| |
Large deflection of plates
The theory described in the above two sections are applicable only for small deflections in which 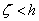 . Here we will derive relations for large deflection of the plate, so that . Here we will derive relations for large deflection of the plate, so that 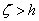 . It should be mentioned here that . It should be mentioned here that 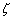 must still be small with respect to the lateral dimension of the plate, must still be small with respect to the lateral dimension of the plate, 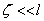 . While for small bending of the plate, . While for small bending of the plate, 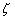 goes from positive to negative, so there is a neutral surface inside the plate, for large deflection, however, bending is also accompanied by stretching, so that there is no such existence of a neutral surface within the plate. Hence, the total energy of the plate in this case includes the pure bending energy and also the energy due to the stretching. In the last two sections we have already considered the two situations of pure bending and pure stretching of the plate; here we will use these results for deriving the equilibrium relations for large deflection of a bent plate. For us, the plate is very thin, a two dimensional surface, and its struction across its thickness is not important. Let goes from positive to negative, so there is a neutral surface inside the plate, for large deflection, however, bending is also accompanied by stretching, so that there is no such existence of a neutral surface within the plate. Hence, the total energy of the plate in this case includes the pure bending energy and also the energy due to the stretching. In the last two sections we have already considered the two situations of pure bending and pure stretching of the plate; here we will use these results for deriving the equilibrium relations for large deflection of a bent plate. For us, the plate is very thin, a two dimensional surface, and its struction across its thickness is not important. Let 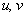 be the in plane displacements along the be the in plane displacements along the 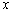 and and 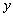 directions respectively and directions respectively and 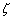 is the transverse displacement due to its bending. Then an element of length is the transverse displacement due to its bending. Then an element of length 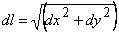 is transformed into an element of length is transformed into an element of length 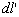 whose square is given by whose square is given by 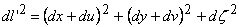 . Substituting in this expression, . Substituting in this expression, 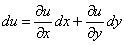 , , 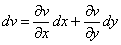 and and 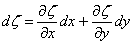 , yields following expression for , yields following expression for 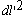 : :
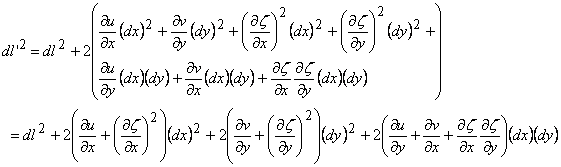 |
(17.6) |
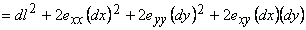 |
(17.7) |
Here we have neglected other quadratic terms in derivatives of displacements 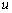 and and 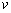 . The same can not be done for . The same can not be done for 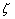 as there is no corresponding first order term. These expressions for the components of strain tensor can now be used in equation (10.17) for finding the expressions for the components of stresses. The corresponding expression for stretching energy is estimated from the following integration as there is no corresponding first order term. These expressions for the components of strain tensor can now be used in equation (10.17) for finding the expressions for the components of stresses. The corresponding expression for stretching energy is estimated from the following integration 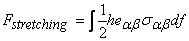 ( ( 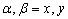 ) over the area of the plate while the bending energy ( ) over the area of the plate while the bending energy ( 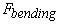 ) is obtained from the equation (10.5). ) is obtained from the equation (10.5).
The total free energy of the plate undergoing large deformation is obtained as, 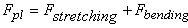
|