The condition of minimum energy requires that 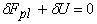 , where , where 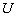 is the potential energy of the external forces and is the potential energy of the external forces and 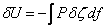 . After some algebraic manipulation, the details of which will not be discussed here, following equations are obtained for finding the displacements . After some algebraic manipulation, the details of which will not be discussed here, following equations are obtained for finding the displacements 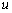 , , 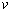 and and 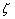 : :
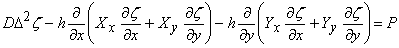
|
(17.8) |
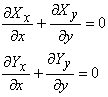 |
(17.9) |
We can introduce the stress function
and simplify equation (10.13a) as,
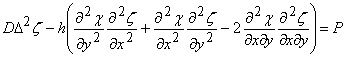 |
(17.10) |
Let us write the strain components in terms of stresses:
In which we can substitute the expressions for the strains from equation 17.6
Deriving the three equations of 10.26 by 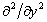 , , 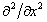 and and 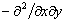 respectively, we obtain, respectively, we obtain,
By adding these three, we obtain,
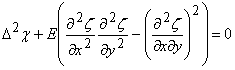 |
(17.13) |
Equations 17.10 and 17.13 represent the complete system of equations for solving problems of large deflections of thin plate. These nonlinear set of equations are called Föppl-von Karman equations. These are not amenable for solving analytically except in some one dimensional cases, so that one needs to use numerical or semi-analytical techniques to handle them. |