In other word 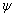 is a harmonic function of the two variables is a harmonic function of the two variables 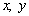 . The boundary condition . The boundary condition 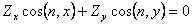 at the curved surface at the curved surface 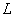 leads to leads to
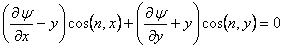 |
(15.8) |
Noting that 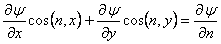 , the b.c. is obtained as , the b.c. is obtained as
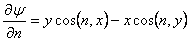 on on 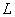 . The problem of finding . The problem of finding 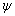 is one of the fundamental problems of the potential theory called “the Neumann problem”. is one of the fundamental problems of the potential theory called “the Neumann problem”.
It can be shown that the resultant of tangential stresses at any cross section is zero:
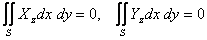 |
(15.9) |
The resultant of moment of external stresses applied to one end is given by
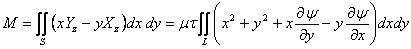 |
(15.10) |
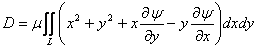
or, 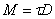 where, where,
the proportionality constant is
called the torsional rigidity of the rod. It is a product of the shear modulus which is a material property of the rod and an integral which depends only upon the shape of the cross section of the rod. Torsional rigidity is always a positive quantity which can be proved from calculating the potential energy stored in the twisted bar. It can also be proved by applying the Green's function.
Let us consider the case of a rod with circular cross section. If the origin is placed at the centre, one has 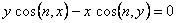 on the boundary. Therefore, on the boundary. Therefore,
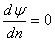 |
(15.11) |
on the entire boundary. Hence 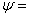 constant which may be taken as 0. In other word in this case the cross sections of the rod remain plane, and the displacements are given as, constant which may be taken as 0. In other word in this case the cross sections of the rod remain plane, and the displacements are given as,
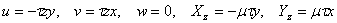 . The torsional rigidity is given by, . The torsional rigidity is given by,
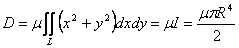 |
(15.12) |
For an annular ring one has, 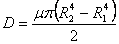 where where 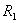 and and 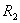 are inner and outer radius respectively. are inner and outer radius respectively. |