Torsional energy
Energy density:
 |
(15.13) |
Total energy =
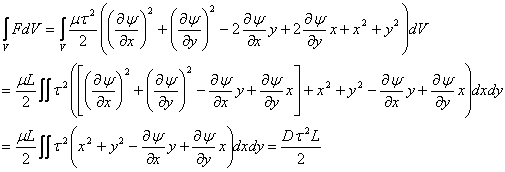 |
(15.14) |
Here we present a propose method by which the function can be estimated for rods of any arbitrary cross-section. In essence we define a new function 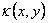 such that it satisfies the following equations: such that it satisfies the following equations:
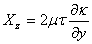 , , 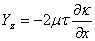 |
(15.15) |
Then from the definition of equation 15.6, we obtain,
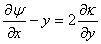 , , 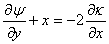 |
(15.16) |
So that,
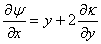 , , 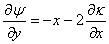 |
(15.17) |
We can then equate the expression for 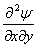 from the above equation, which results in the following relation: from the above equation, which results in the following relation:
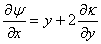 , , 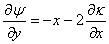 |
(15.17) |
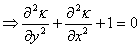 |
(15.18) |
Equation 9.18 is interesting as it is akin to the soap film equation written as,
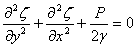 |
(15.19) |
Here we consider that a hole of an arbitrary shape is cut into a solid plate and a soap film is allowed to form by dipping the plate inside a soap solution and then withdrawing it out. The soap film does not remain flat but assumes a curved shape because of pressure difference 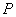 between the two sides of the soap film. We can then obtain the displacement between the two sides of the soap film. We can then obtain the displacement 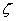 of the film at various location of the film at various location 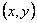 which satisfies equation 9.19. Notice that we can recover equation 9.18 by simply substituting, which satisfies equation 9.19. Notice that we can recover equation 9.18 by simply substituting,
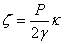 |
(15.20) |
This result then suggests a simple way to obtain the function 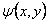 : we can form a hole of the shape of the cross-section of the rod in a rigid plate and then obtain apply different amount of differential pressure : we can form a hole of the shape of the cross-section of the rod in a rigid plate and then obtain apply different amount of differential pressure 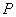 across the film and obtain the displacement across the film and obtain the displacement 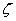 . We obtain the function . We obtain the function 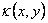 from this data by using equation 9.20, following which we can obtain from this data by using equation 9.20, following which we can obtain 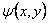 from the set of relations in 15.17 from the set of relations in 15.17
|