Let's consider a straight rod with arbitrary cross section whose co-ordinate system is as follows: while the 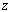 axis remains along the axis of the rod, its origin is somewhere inside and the axis remains along the axis of the rod, its origin is somewhere inside and the 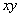 plane can be taken as the undisplaced cross section.. We define the torsion angle plane can be taken as the undisplaced cross section.. We define the torsion angle 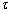 as the angle through which the rod is twisted per unit length, so that two neighboring elements as the angle through which the rod is twisted per unit length, so that two neighboring elements 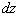 distance apart turns through an angle distance apart turns through an angle 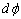 : : 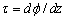 . . 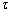 is rather small so that when this distance is of the order of the transverse dimension is rather small so that when this distance is of the order of the transverse dimension 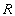 of the rod, it satisfies of the rod, it satisfies 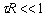 . Let's estimate the displacements . Let's estimate the displacements 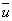 in a small portion of the rod near the origin of the rod. When the radius vector in a small portion of the rod near the origin of the rod. When the radius vector 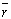 turns through an angle turns through an angle 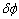 , the displacement of its end is given by , the displacement of its end is given by
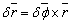 |
(15.2) |
where 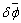 is the vector whose magnitude is the angle of rotation and direction is that of the axis of rotation i.e. the is the vector whose magnitude is the angle of rotation and direction is that of the axis of rotation i.e. the 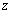 axis. For points with coordinates axis. For points with coordinates 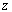 relative to the relative to the 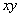 plane the angle of rotation is plane the angle of rotation is 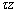 , hence, the components , hence, the components 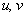 and and 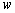 of the displacement vector along the of the displacement vector along the  and and 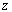 directions respectively are, directions respectively are,
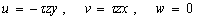 |
(15.3) |
It is easy to see that the components of the stress tensor calculated from these displacements satisfy the stress equilibrium relations and the boundary conditions.
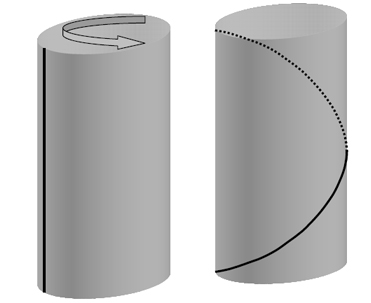
In general points undergo displacement along the 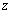 axis also. Let's assume that for small axis also. Let's assume that for small 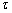 , this displacement is, , this displacement is,
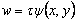 |
(15.4) |
Here 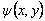 is a single valued function, called the torsion function, which signifies that any cross section of the rod does not remain planer bur become curved. Furthermore, the origin of the co-ordinate system which was fixed at a particular point in the is a single valued function, called the torsion function, which signifies that any cross section of the rod does not remain planer bur become curved. Furthermore, the origin of the co-ordinate system which was fixed at a particular point in the 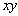 plane can now move along the plane can now move along the 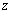 co-ordinate. Then the components of the strain tensor are as follows: co-ordinate. Then the components of the strain tensor are as follows:
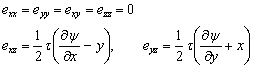 |
(15.5) |
it should be noted that 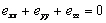 , signifying that torsion does not result in change in volume, it is a pure shear deformation. Components of stress tensor are, , signifying that torsion does not result in change in volume, it is a pure shear deformation. Components of stress tensor are,
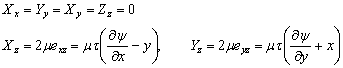 |
(15.6) |
Then the general equation of equilibrium reduces to,
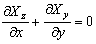 |
(15.7) |
in which substitution of the expressions in (15.5) results in the two dimensional Laplacian:
|