Bending of a rod with circular cross-section:
When a rod of arbitrary cross-section is bent, it undergoes also twisting although no external twisting moment may have been applied at the end. However for a circular rod no torsion results from bending. We can show this result from our earlier derivations. Consider the following derivative:
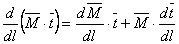 |
(13.5) |
Now 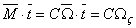 and and 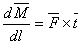 . Here . Here 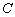 is called the torsional rigidity. is called the torsional rigidity.
Substituting these expressions we have,
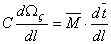 |
(13.6) |
Noting that for a rod with circular cross-section, 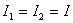 , , 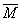 can be written as can be written as
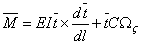 |
(13.7) |
which when substituted in eqn. (13.6) yields,
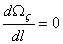 or or 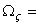 constant, i.e. torsion angle is constant along the length of the rod. Hence if no twisting moment is applied at the end of the rod, constant, i.e. torsion angle is constant along the length of the rod. Hence if no twisting moment is applied at the end of the rod, 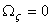 . Hence pure bending of a rod with circular cross-section, we can write, . Hence pure bending of a rod with circular cross-section, we can write,
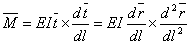 |
(13.8) |
Substitution of eqn. (13.8 ) into eqn. (11.17) yields,
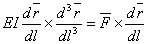 |
(13.9) |
For simple bending of the rod about the 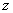 axis, the above expressions can be simplified by writing the tangent in terms of angle axis, the above expressions can be simplified by writing the tangent in terms of angle 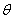 it makes with the it makes with the 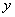 axis: axis:
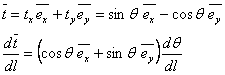 |
(13.10) |
Similarly, the expression for the torque and its derivative can be written as,
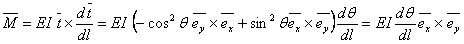
|
|
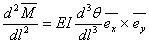 |
(13.11) |
|