| |
Bending of a rod under distributed load
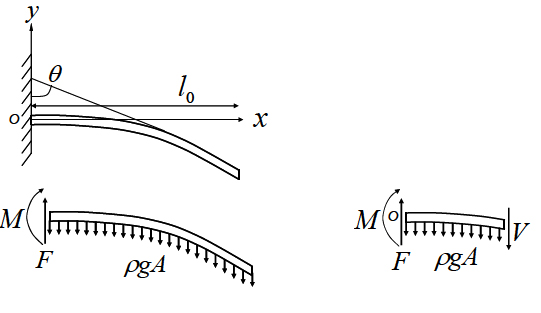
Here we will consider large bending of a rod which remains strongly attached to a rigid wall. Let us say that the rod of length 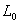 and area of cross-section and area of cross-section 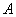 bends under the action of a uniform load, e.g. gravity. If the density of the rod is bends under the action of a uniform load, e.g. gravity. If the density of the rod is 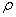 , then assuming that the rod does not undergo any extension, the reaction force at the rigid wall can be written as: , then assuming that the rod does not undergo any extension, the reaction force at the rigid wall can be written as:
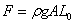 |
(13.12) |
At the free end of the rod it is not acted upon by any reaction force. Say at any cross-section at a length 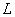 from wall, the reaction force is from wall, the reaction force is 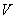 , then from force balance, , then from force balance,
Integrating the vectorial form of above expression,
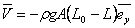 and and 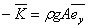 |
(13.14) |
From equation 13.14, 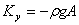 For a circular rod 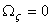 , we have, , we have,
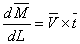 , so that, , so that, 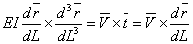 |
(13.15) |
Now

|
(13.16a) |
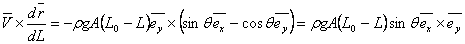 |
(13.16a) |
Thus from equation 13.16a and b we can write the following force balance equation for bending of the rod
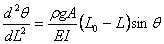 |
(13.17) |
Putting 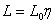 and and 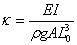 , we have , we have 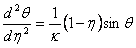 This equation is solved with the following boundary conditions:
Solution of equation 13.17 along with the b.c. 13.18 yields the following graph, 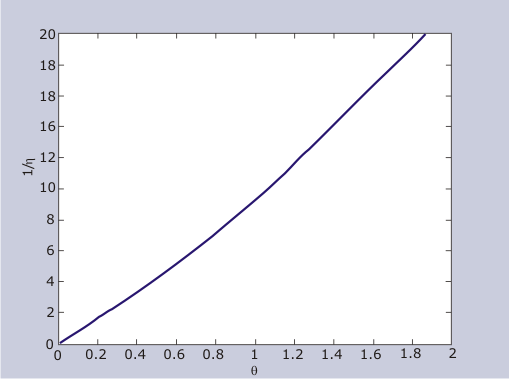
|