The equations of equilibrium of rods

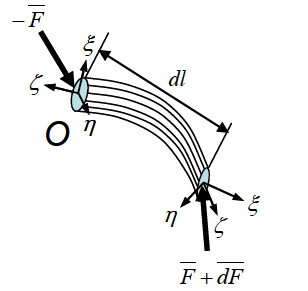
Consider an infinitesimal element of length bounded by two adjacent cross-sections of the rod. Let be the resultant internal stress on a cross section; then the force acting on this cross-section of the rod is and that acting on the other end is . If is the external force acting per unit length of the rod, then, the total force acting on the element of length is . Since the rod is in equilibrium under the action of these two forces, we have,

or

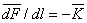(13.1)

Similarly, the moment of the internal stresses are and respectively. And moment of the internal stresses about point O' is . Summing up the total moments is obtained as:

(13.2)

Dividing by and noting that : the unit vector tangential to the rod, we have

(13.3)

If is a concentrated force applied only at its free end, then = constant. Furthermore, putting and by integrating, we have constant

Similarly, we can differentiate equation 13.3 with respect to to obtain

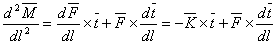(13.4)