The energy of a bent rod
We have so far discussed the bending deformation of only a small portion of the rod; however as we discuss the deformation whole through the rod, we will immediately see that the deformation does not remain small, rather the rod undergoes large bending deformations. Furthermore bending of the rod is also accompanied by some torsion, so that the rod undergoes both bending and twisting deformations.
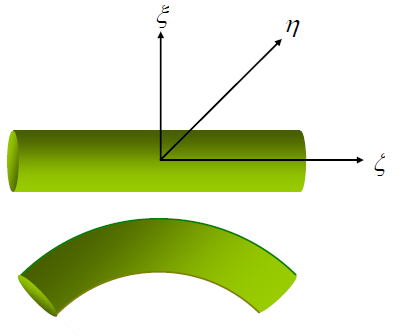
To describe the deformation we divide the rod into infinitesimal elements each of which is bounded by two adjacent cross-sections. For each such element we choose a co-ordinate system 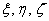 so that in the un-deformed state all these systems are parallel to each other and their so that in the un-deformed state all these systems are parallel to each other and their 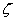 axes is parallel to the axis of the rod but in the deformed state the co-ordinate system for each element is rotated infinitesimally relative to each other. axes is parallel to the axis of the rod but in the deformed state the co-ordinate system for each element is rotated infinitesimally relative to each other.
Let 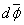 be the vector of the angle of relative rotation of two systems at a distance be the vector of the angle of relative rotation of two systems at a distance 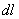 apart along the rod. The infinitesimal angle of rotation can be regarded as vector the components of which are the angles of rotation about the three axes of co-ordinates. We define a vector apart along the rod. The infinitesimal angle of rotation can be regarded as vector the components of which are the angles of rotation about the three axes of co-ordinates. We define a vector
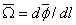 |
(12.8) |
which is the rate of rotation of the co-ordinate axes along the rod. If the deformation is pure rotation, then 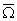 is the vector parallel to the axis of the rod and is magnitude is the torsion angle is the vector parallel to the axis of the rod and is magnitude is the torsion angle 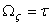 . If the plane of bending is . If the plane of bending is 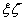 the rotation is about the the rotation is about the 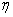 axis, i.e. axis, i.e. 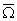 parallel to the parallel to the 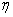 axis. axis.
|