Other components of the strain tensor are zero, so that:
 |
(12.3) |
Integrating, the displacements can be given as
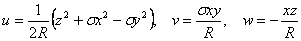 |
(12.4) |
The formulae for the displacements show that the cross-sections remain plane but the planes are rotated so that they pass through the centre of curvature. Shape of the cross-sections is changed. For example if the cross sections initially are rectangular with boundaries 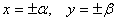 in a plane in a plane 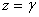 , these boundaries will become the curves given respectively by, , these boundaries will become the curves given respectively by,
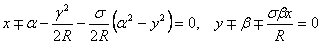 |
(12.5) |
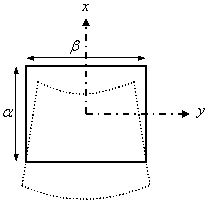
For a rod with rectangular cross-section (sides 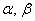 ) the principal moments of inertia are ) the principal moments of inertia are
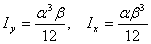 |
(12.6) |
For a rod with circular cross-section, with radius 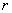 , the moment of inertia is , the moment of inertia is
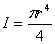 |
(12.7) |
|