Bending of a rod by couples applied at its ends:

The rod is placed horizontally and is bent by applying a couple at its end as shown in the figure. In the small bending limit, the rod is stretched in the convex side, whereas in the concave side it is under compression. The neutral surface lying in the 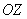 plane separates these two regions. plane separates these two regions.
Here by small bending we mean that the deformation as well as the strain is small. Similar to bending of plates, external forces on the sides of the rod are small with respect to the internal stresses, so that at its sides, we have 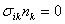 which ultimately results in that the all the components of the stress tensor except which ultimately results in that the all the components of the stress tensor except 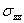 is zero. Let there be a small element is zero. Let there be a small element 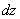 lying along the lying along the 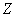 axis at a distance axis at a distance 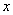 from the neutral surface. On bending the length of this element becomes from the neutral surface. On bending the length of this element becomes 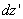 . The elements . The elements 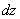 and and 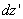 lie on arcs of radii lie on arcs of radii 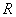 and and 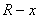 respectively. Then it can be easily shown that respectively. Then it can be easily shown that
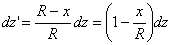 |
(12.1) |
so that the relative expansion is 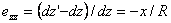 . We now find . We now find 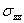 as as 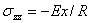 . The resultant traction over any cross-section is . The resultant traction over any cross-section is 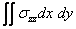 and it is equal to zero if the and it is equal to zero if the 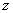 axis coincides with the line of centroid of the normal section. The component of the couple about the axis coincides with the line of centroid of the normal section. The component of the couple about the 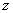 axis vanishes. However, that about the axis vanishes. However, that about the 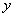 axis is nonzero and is axis is nonzero and is 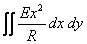 or or 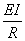 where where 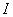 is the moment of inertia of the section about an axis through its centroid parallel to the is the moment of inertia of the section about an axis through its centroid parallel to the 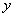 axis. Two more components of the strain tensor besides axis. Two more components of the strain tensor besides 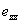 are non-zero: they are, are non-zero: they are,
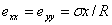 |
(12.2) |
|