Let the unit vector 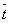 is tangential to the rod. Then the derivative is tangential to the rod. Then the derivative 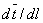 is the curvature to the line: is the curvature to the line: 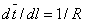 . .
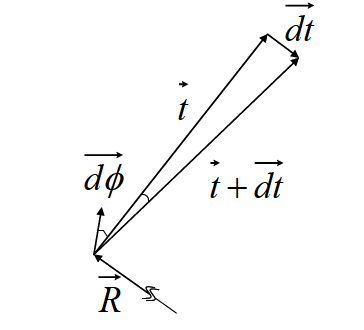
The change in a vector due to infinitesimal rotation is the vector product of the rotation vector and the vector itself: 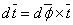 , or dividing by , or dividing by 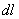
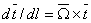 |
(12.9) |
Vector multiplication by 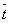 gives gives
or
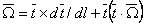 |
(12.10) |
Since the tangent vector points in the direction of the 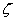 axis of the rod, axis of the rod, 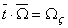 . Say the unit vector . Say the unit vector 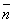 points to the principal normal: points to the principal normal: 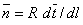 , then we have: , then we have:
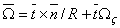 |
(12.11) |
The unit vector 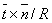 is a binormal vector with components is a binormal vector with components 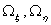 so that its magnitude is equal to the curvature so that its magnitude is equal to the curvature 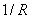 . For plane curves, binormal vector is the unit vector normal to the plane. Principal normal is the usual normal to the curve directed towards the center of curvature at that point. Since the elastic energy of the rod is a quadratic function of deformation, in this case it will be function of the components of the vector . For plane curves, binormal vector is the unit vector normal to the plane. Principal normal is the usual normal to the curve directed towards the center of curvature at that point. Since the elastic energy of the rod is a quadratic function of deformation, in this case it will be function of the components of the vector 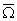 . However, these terms should not contain the expressions . However, these terms should not contain the expressions 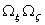 and and  as they are dependent on the direction of the as they are dependent on the direction of the 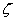 axis. Finally if we have axis. Finally if we have 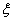 and and 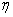 axes coinciding with the principal axes of inertia, then we should not have also the term axes coinciding with the principal axes of inertia, then we should not have also the term 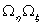 .The total energy of the rod then consists of that due to torsion about the .The total energy of the rod then consists of that due to torsion about the 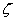 axis and bending about the axis and bending about the 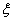 and and 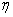 axes: axes:
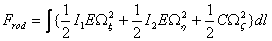 |
(12.12) |
The moment applied about the 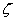 axis, axis, 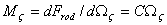 . Other components of the moment, can similarly be obtained as, . Other components of the moment, can similarly be obtained as,
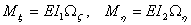 |
(12.13) |
And the elastic energy in terms of the moments are,
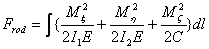 |
(12.14) |
|