Transformation of components of strain (contd...)
If the axes are so chosen that they coincide with the principal axes of the surface then, 1.32 takes the form: 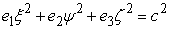 , where , where 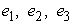 are the are the 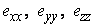 of the new axes. of the new axes.
Principal axes are the roots of the equation:
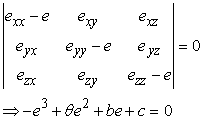 |
(1.32) |
where 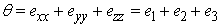 is an invariant, since coefficients of 1.32 should be so. is an invariant, since coefficients of 1.32 should be so.
Consider a right parallelepiped having sides OA= 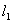 , OB = , OB = 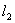 and OC= and OC= 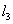 . Then its volume is . Then its volume is 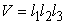 . After deformation the right parallelepiped remains a right parallelepiped with sides . After deformation the right parallelepiped remains a right parallelepiped with sides 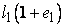 , , 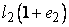 , , 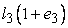 , hence its volume is , hence its volume is
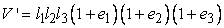 = = 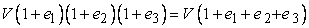 |
(1.33) |
So that,
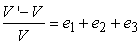 |
(1.34) |
Hence 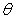 is the relative expansion in volume or the cubical expansion. is the relative expansion in volume or the cubical expansion.
In a more general form, the ratio of a volume element in strained state to unstrained state is given as
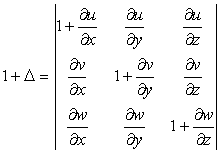 |
(1.35) |
where 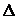 is the cubical dilation. is the cubical dilation.
|