Saint-Venant's conditions of compatibility :
We have so far deduced the formula for components of strain to be calculated from the components of displacements which are functions of the current location 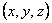 of a point. of a point.
Let us now look at the inverse problem: say, the components of strain exx ,...,eyy,... in a body are known, then how to determine the components of displacements u,v,w.
This problem can not be solved in a straight forward manner, because, say somehow we are able to find out the components 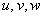 , but then if we add an arbitrary displacement to them, then, it does not change the strain components, because strain does not depend upon the rigid body translation. , but then if we add an arbitrary displacement to them, then, it does not change the strain components, because strain does not depend upon the rigid body translation.
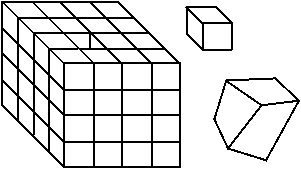
Consider the following situation: Let's say we separate an infinitesimal cube from a body and subject it to deformations resulting in a parallelepiped. We can subject many other cubes to such deformations. Now we put them all back to the body.
Question is will the adjoining faces and lines will perfectly match without any gaps, after this exercise. It will almost be impossible to do that. Hence, it is obvious now that components of strain must satisfy certain conditions in order to result in deformations without discontinuities.
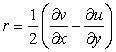 , |
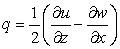 and |
|
where 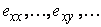 are single valued functions having continuous second order derivatives. are single valued functions having continuous second order derivatives.
One has six equations and three unknown functions, which implies that the problem may not have solutions if 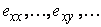 are not subjected to additional conditions. are not subjected to additional conditions. |