Transformation of components of strain:
Consider 1.17, here 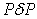 is a quadratic with respect to is a quadratic with respect to 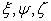 . But since . But since 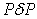 has a definite meaning, it should be independent of the choice of coordinate axes or of the transformation of coordinates. has a definite meaning, it should be independent of the choice of coordinate axes or of the transformation of coordinates.
In other word, if 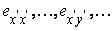 are the components of strain in the new coordinate system and if are the components of strain in the new coordinate system and if 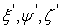 are the component of the vector are the component of the vector 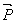 , then we have: , then we have:
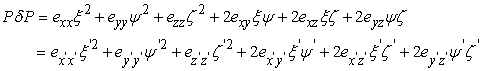 |
(1.26) |
Now let's say 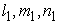 are the direction cosines of the are the direction cosines of the 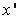 axis new coordinate system with respect to the old one and like wise. We can then develop following table: axis new coordinate system with respect to the old one and like wise. We can then develop following table:
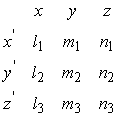 |
(1.27) |
The coordinate of the vector 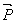 in the old system can be expressed with respect to the new one as, in the old system can be expressed with respect to the new one as,
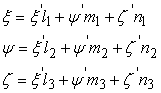 |
(1.28) |
Substituting this into 1.26 and then matching the coefficients for 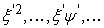 in the left and right hand sides, in the left and right hand sides,
 |
(1.29) |
Furthermore we can rewrite 1.17 as,
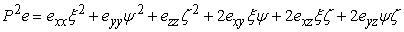 |
(1.30) |
where 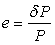 is the relative increase in length of vector is the relative increase in length of vector 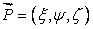 . Since . Since 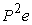 does not depend on any direction but only its magnitude, hence for every direction, does not depend on any direction but only its magnitude, hence for every direction, 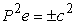 , where C is an arbitrary constant with the dimension of length. If the starting point of P lies on the origin, then its other end point lies on the surface , where C is an arbitrary constant with the dimension of length. If the starting point of P lies on the origin, then its other end point lies on the surface 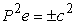 , or , or
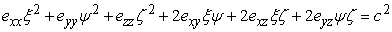 |
(1.31) |
which is called the strain surface.
|