General Expressions of strain:
Let the new position of the point is given in terms of the deformations as 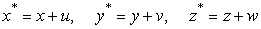 in the strained state. in the strained state.
Consequently, the particle which was on a given curve in the unstarined state, now belongs to a different curve in the strained state. If 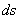 be a differential element in the original curve, then direction cosines of a tangent at any point on it are be a differential element in the original curve, then direction cosines of a tangent at any point on it are 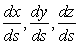 . Direction cosines of a tangent on an elemental arc . Direction cosines of a tangent on an elemental arc 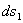 in the strained curve are in the strained curve are 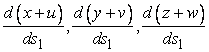 . Then, . Then,
However, the direction cosines are
From the expressions of equation 1,
Noting that

we have the following eqn,
where 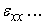 are the following, are the following,
We thus obtain the general expressions for the components of strain in terns of the gradients of displacements.
The left hand side of 1.24 is a constant and the right hand side signifies an ellipsoid. It has the property that in any direction, the length of its radius is inversely proportional to 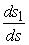 . Such an ellipsoid is called the reciprocal strain ellipsoid . . Such an ellipsoid is called the reciprocal strain ellipsoid .
|