IV.5.2: Bode Stability Criterion
Consider a simple first order plus dead time process to be controlled by a proportional controller:
|
|
Fig. IV.14: Example of first order system for studying Bode stability criterion |
|
The open-loop transfer function for this system is given by
(IV.71) |
The Bode plot of the above open loop transfer function is given by the following figure.
|
We are interested to know the frequency where the phase shift is ![]() . Numerically it can be solved by the equation
. Numerically it can be solved by the equation
(IV.72) |
The frequency is ![]() and the value of
and the value of ![]() at
at ![]() is observed to be
is observed to be ![]() which can also be found numerically by,
which can also be found numerically by,
(IV.73) |
The above exercise indicates that in order to obtain ![]() at this frequency
at this frequency ![]() one needs to set the value of
one needs to set the value of ![]() as,
as,
(IV.74) |
At this juncture, one needs to perform a thought experiment in order to understand the Bode stability criterion. Let us set the value of controller gain, ![]() and let us “open up” the feedback loop as indicated in the figure before. Suppose, we vary the setpoint as a sinusoidal function
and let us “open up” the feedback loop as indicated in the figure before. Suppose, we vary the setpoint as a sinusoidal function ![]() . As the loop is open, the error will be equal to the setpoint
. As the loop is open, the error will be equal to the setpoint ![]() and thereby yield an output,
and thereby yield an output,
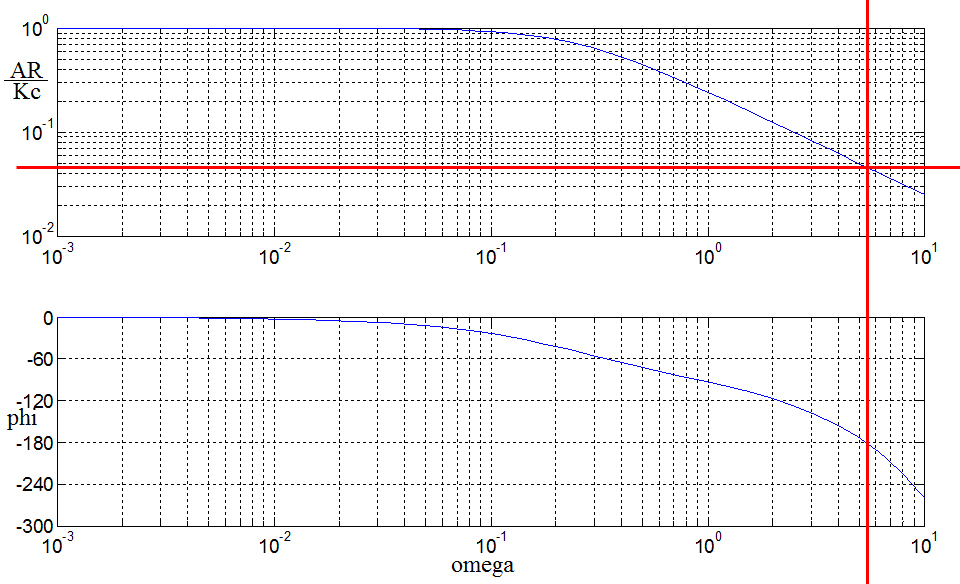 Fig. IV.15: Bode plot
Fig. IV.15: Bode plot