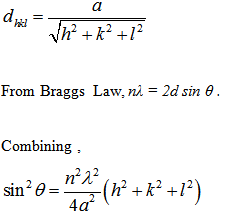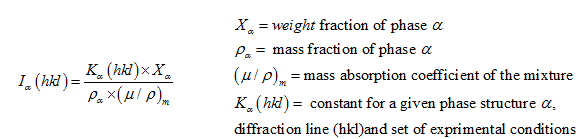
Peak intensities are generally measured from peak heights on the assumption that peak height is proportional to peak area

2.  Determination of average crystallite size

Ideally, a Bragg diffraction peak is a line without width. In reality, diffraction from a crystal specimen produces a peak with a certain width. This is known as peak broadening. The peak width depends on the size of the crystals. Peak width is inversely related to crystal size; that is, peak width increases with decreasing crystal particle size.

The average crystallite size can be determined by Scherrer formula using elementary line broadening analysis. The Scherrer formula assumes that the breadth of the diffraction peak of crystallites (small single crystals) mainly depends on the characteristics of crystallites (size and the defect in the lattice). Elementary analysis of the broadening assumes that lattice deformation is negligible. According to Scherrer, the thickness of crystallite, L, can be determined by

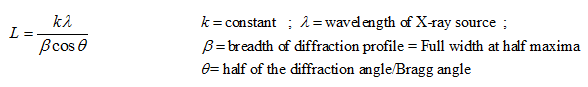
The diffraction corresponding to the most intense peak is selected to calculate the average crystallite size using Scherrer relation. The Scherrer formula assumes that crystallite size is the major source leading to line broadening effects of the diffractions peaks, but there is always a broadening can also be due to instrumental factors such as slit width, sample size, imperfect focusing or misalignment of diffractometers.

3.  Spacing between atomic planes of a crystal

Based on Bragg's Law, information on spacing between atomic planes can be obtained when constructive interference occurs. Knowing the spacing of crystallographic planes by diffraction methods, the crystal structure of materials can be determined. The plane spacing of cubic crystal is related to the lattice parameter (a) by the following equation.