Extended Langmuir model for adsorption in a multi-adsorbate system
The Langmuir model is also used to evaluate adsorption equilibrium data in a multi-adsorbate system and is known as extended Langmuir model. The extended Langmuir model mostly has been used to evaluate adsorption equilibrium data in binary system. The extended Langmuir model was first proposed by Butler and Ockrent [1]. Their model was based on the same assumptions as that of Langmuir model for single adsorbates. That is the model assumed (i) a homogeneous surface with respect to the energy of adsorption, (ii) no interaction between adsorbed species, and (iii) that all adsorption sites are equally available to all adsorbed species. Assuming the rate of adsorption of a species at equilibrium is equal to its rate of desorption, the following equations were derived.
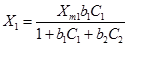--------------------[7]
--------------------[8]
Where, the X1 and X2 are the amount of solute 1 and solute 2 respectively, which are absorbed per unit weight or per unit surface area of absorbent at equilibrium concentrations C1 and C2, respectively. The Xm1 and Xm2 are the maximum values of X1 and X2, respectively, that can be obtained in single solute system and correspond to monolayer coverage of the adsorbent. The b1 and b2 are constants and function of the energy of adsorption of solutes 1 and 2, respectively, in a single solute system.
When some of the adsorption sites are inaccessible or unavailable to one type of solute in a bisolute system then, a fraction of the adsorption occurs without competition that is Xm1 ≠ Xm2. Jain and Snoeyink [2] proposed the following equations taking into account adsorptions with and without competition.
------------[9]
------------------------------------------------------------[10]
The first term on the right hand side of Eq. 9 is the number of molecules of solute 1 that adsorb without competition on the surface area proportional to (Xm1 -Xm2). The second term represents the number of solute 1 adsorbed on the surface area proportional to Xm2 under competition with solute 2 and is based on the Langmuir model for competitive adsorption. The number of molecules of solute 2 adsorbed on surface area proportional to Xm2 under competition with solute 1 can be calculated from Eq.10.
Book References :
• J.J. Carberry, Chemical and catalytic reaction Engineering, Dover Publications, 2001
• J. M. Thomas & W. J. Thomas , Principles and Practice of Heterogeneous Catalysis, VCH, 1997
• J. M. Smith, Chemical Engineering Kinetics, McGraw-Hill Book Company, 1981
• R. J. Farrauto & C. H. Bartholomew, Fundamentals of Industrial catalytic Processes, Blackie Academic & Professional, 1997
• D.M. Ruthven, Principle of adsorption & adsorption processes, John Wiley & sons, 1984.
Publication reference
1. J. A. V Butler, C Ockrent, J. Phys. Chem. 34( 1930) 2841-2845.
2. J. S Jain, V. L. Snoeyink, J. Water Pollut. Control Fed. 45( 1973) 2463-2479.