:
Constitutive Equations

The relationship between stress and strain is known as constitutive equation. The general form of this equation is

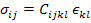(2.34)

Here, 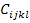 are called elastic constants. This is also referred to as elastic moduli or elastic stiffnesses. This form of constitutive equation is known as generalized Hooke’s law. Very soon, we will see this equation in detail for various material types.
The inverse of this equation can be written as

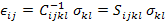(2.35)

where 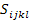 is known as compliance.

Plane Stress Problem

Plane stress problem corresponds to a situation where out of plane stress components are negligibly small. Thus, we can say that the state of stress is planar. The planar state of stress in x-y plane is shown in Figure 2.6. For the case shown in this figure, the normal and shear stress components in z directions, that is 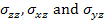 are zero. Please note that the state of stress shown in this figure assumes the stress symmetry.

Note: A careful observation for strain components in z direction (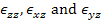) reveals that these need not be zero. This is a common mistake made by many readers. The magnitude of these strain components can be found with the help of constitutive equation given in Equation (2.34).

For plane stress problem the equilibrium equations take the following form

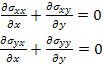(2.36)

Plane Strain Problem

Plane strain problem corresponds to a condition where all the out of plane strain components are negligibly small. Here, we denote 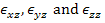as out of plane strain components. The readers are again cautioned to note that the out of plane stress components need not be zero. These depend upon the constitutive equation. Further, the equilibrium equation is same as Equation (2.36) and 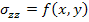.