Principles from Work and Energy

Strain Energy Density

            The strain energy stored in a body per unit volume is called as strain energy density. In the absence of internal energy, the strain energy density for a linearly elastic body is given as

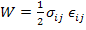(2.37)

The expanded form of the above equation using symmetry of stress and strain components is

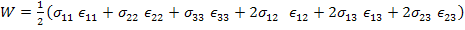(2.38)

The readers should note that strain energy density is a scalar quantity. Further, it is a positive definite quantity.

Principle of Minimum of Total Potential Energy

The principle of minimum of total potential energy states that of all possible kinematically admissible displacement fields, the actual solution to the problem is one which minimizes the total potential energy .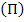
The total potential energy (for linearly elastic material) is defined as

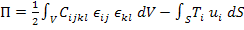(2.39)

Note: The kinematically admissible displacement field is a single valued and continuous displacement field that satisfies the displacement boundary condition.

Principle of Minimum of Total Complementary Potential Energy

The principle of minimum of total complementary potential energy states that of all possible statically admissible stress fields, the actual solution to the problem is one which minimizes the total complementary potential energy .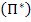
The total complementary potential energy (for linearly elastic material) is defined as

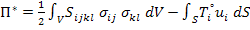(2.40)

Note: The statically admissible stress field is one that satisfies both equilibrium equations and traction boundary condition.