| |
Equilibrium Equations
The equilibrium equations for a body to be in static equilibrium at a point are given in index notations as
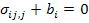 |
(2.29) |
where, 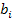 are the body forces per unit volume. If the body forces are absent, then the equilibrium equation becomes are the body forces per unit volume. If the body forces are absent, then the equilibrium equation becomes
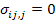 |
(2.30) |
The equilibrium equations, without body forces are written using xyz coordinates as follows:
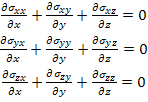 |
(2.31) |
Boundary Conditions
The boundary conditions are very essential to solve any problem in solid mechanics. The boundary conditions are specified on the surface of the body in terms of components of displacement or traction. However, the combination of displacement and traction components is also specified.
Figure 2.5 shows a body, where the displacement as well as traction components are used to specify the boundary conditions.
We define traction vector 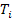 for any arbitrary point (for example, point P in Figure 2.5) on surface as a vector consisting of three stress components acting on the surface at same point. Here, the three stress components are normal stress for any arbitrary point (for example, point P in Figure 2.5) on surface as a vector consisting of three stress components acting on the surface at same point. Here, the three stress components are normal stress 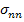 and shear stress and shear stress 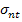 and and 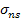 . The traction vector at this point is written as . The traction vector at this point is written as
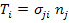 |
(2.32) |
where 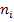 is the ith component of the unit normal to the surface at point P. For example, if this surface is perpendicular to axis 2, then is the ith component of the unit normal to the surface at point P. For example, if this surface is perpendicular to axis 2, then 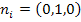 and the components of traction acting at a point on this surface are given as follo and the components of traction acting at a point on this surface are given as follows
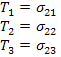 |
(2.33) |
Figure 2.5: (a) A body showing displacement and traction boundary conditions, (b) Traction vector at any arbitrary point P on the surface of a body |
|