The engineering shear strain components are given as follows:
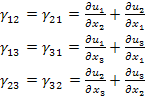 |
(2.25) |
Using the engineering shear strain components, the strain tensor can be written in matrix form as
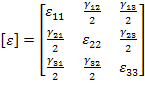 |
(2.26) |
Stress
Now, we will introduce the concept of stress. The components of stress at a point (also called State of Stress) are (in the limit) the forces per unit area which are acting on three mutually perpendicular planes passing through this point. This is represented in Figure 2.4. Stress tensor is a second order tensor and denoted as 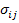 . In this notation, the first subscript corresponds to the direction of the normal to the plane and the second subscript corresponds to the direction of the stress. For example, . In this notation, the first subscript corresponds to the direction of the normal to the plane and the second subscript corresponds to the direction of the stress. For example, 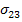 denotes the stress component acting on a plane which is perpendicular to direction 2 and stress is acting in direction 3. The tensile normal stress components denotes the stress component acting on a plane which is perpendicular to direction 2 and stress is acting in direction 3. The tensile normal stress components 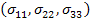 are positive. The shear stress components are positive. The shear stress components 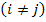 are defined to be positive when the normal to the plane and the direction of the stress component are either both positive or both negative. are defined to be positive when the normal to the plane and the direction of the stress component are either both positive or both negative.
The readers should note that the state of stress shown in Figure 2.4 represents all stress components in positive sense. In this figure, the stress components are shown on positive faces only.
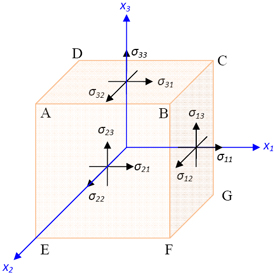 |
| Figure 2.4 State of stress at a point |
The stress tensor can be written in matrix form as follows:
 |
(2.27) |
In general, instead of using global 1-2-3 coordinate system, x-y-z global coordinate system is used. Further, the shear stress components are shown using notation 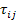 . Thus, the stress tensor in this case can be written as . Thus, the stress tensor in this case can be written as
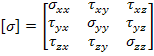 |
(2.28) |
Note: The stress tensor will be symmetric, that is 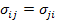 only when there are no distributed moments in the body. The readers are suggested to read more on this from any standard solid mechanics book. In this entire course, we will deal with symmetric stress-tensor. only when there are no distributed moments in the body. The readers are suggested to read more on this from any standard solid mechanics book. In this entire course, we will deal with symmetric stress-tensor.
|