|
Now, we will define strain tensor. We are going to find 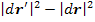 . We know that . We know that 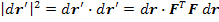 . Thus, . Thus,
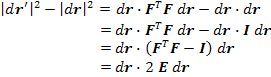 |
(2.16) |
where E is Lagrangian Strain Tensor. Now using the last two of Equation (2.16) for 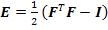 we get, we get,
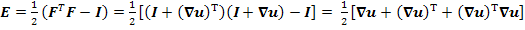 |
(2.17) |
This equation can be written in index form as
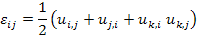 |
(2.18) |
where 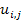 is given as is given as 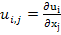 . Thus, the strain components are nonlinear in . Thus, the strain components are nonlinear in 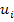 . Here, . Here, 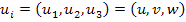 are the displacement components in three directions. For example, let us write the expanded form of strain components are the displacement components in three directions. For example, let us write the expanded form of strain components 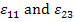 . .
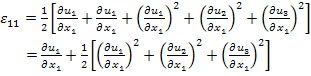 |
(2.19) |
Similarly,
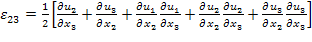 |
(2.20) |
The readers should observe that from the definition of strain tensor in Equation (2.18), the strain tensor is symmetric (that is, 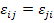 ). If the gradients of the displacements are very small the product terms in Equation (2.18) can be neglected. Then, the resulting strain tensor (called Infinitesimal Strain Tensor) is given as ). If the gradients of the displacements are very small the product terms in Equation (2.18) can be neglected. Then, the resulting strain tensor (called Infinitesimal Strain Tensor) is given as
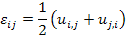 |
(2.21) |
The individual strain components are given as
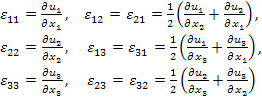 |
(2.22) |
The readers are very well versed with these definitions. This strain tensor can be written in matrix form as
 |
(2.23) |
Note: The shear strain components mentioned above are tensorial components. In actual practice, engineering shear strains (which are measured from laboratory tests) are used. These are denoted by 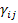 . The relation between tensorial and engineering shear strain components is . The relation between tensorial and engineering shear strain components is
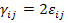 |
(2.24) |
|