Analysis of Concentric Cylinders
When the concentric cylinders are subjected to either an axial load or a uniform radial stress then there are no shear stresses produced. Further, in an infinite cylinder away from the ends, the stresses are independent of 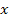 . For this state of stress, there will be one equilibrium equation given as . For this state of stress, there will be one equilibrium equation given as
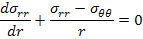 |
(7.169) |
where, 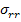 and and 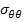 are radial and circumferential stresses, respectively. For a cylindrical coordinate system with no shear stresses, we can write normal stresses for transversely isotropic material as are radial and circumferential stresses, respectively. For a cylindrical coordinate system with no shear stresses, we can write normal stresses for transversely isotropic material as
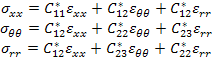 |
(7.170) |
Similarly, for transversely isotropic fibre and isotropic matrix the normal stresses are given as
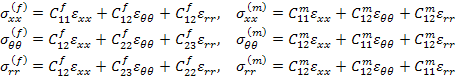 |
(7.171) |
Now, we write the strain displacement relations in cylindrical coordinates as
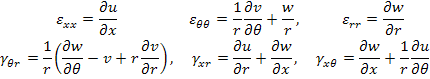 |
(7.172) |
where, 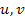 and and 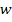 are axial, circumferential or tangential and radial displacements, respectively. Further, with no shear effects and axisymmetry the tangential displacement is zero. It should be noted that the stresses are not function of are axial, circumferential or tangential and radial displacements, respectively. Further, with no shear effects and axisymmetry the tangential displacement is zero. It should be noted that the stresses are not function of 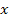 . Hence, the strains are independent of . Hence, the strains are independent of 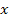 . Hence, the displacement . Hence, the displacement 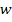 can be a function of can be a function of 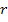 . However, . However, 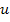 can be function of can be function of 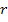 and, at most, a linear function of and, at most, a linear function of 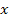 . Hence, in the expression for strain . Hence, in the expression for strain 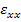 there is partial derivative and not in the expression for there is partial derivative and not in the expression for 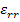 . For the expression of . For the expression of 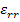 we have the full derivative with respect to we have the full derivative with respect to 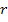 . .
Thus, the normal strains for the displacements in this case simplify to
When these strain-displacement relations are used in stress-strain relations then the equilibrium equation in Equation (7.169) gives an ordinary differential equation in 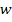 as as
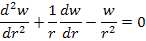 |
(7.173) |
|