|
Now we define the effective Poisson’s ratios 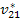 and and 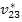 as as
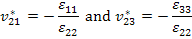 |
(7.162) |
Thus, using Equation (7.149), we get
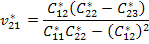 |
(7.163) |
and
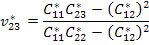 |
(7.164) |
Further, from the symmetry consideration we have the following relations
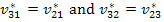 |
(7.165) |
and from the reciprocal relations
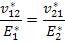 |
(7.166) |
Thus, we can write the following useful relations as
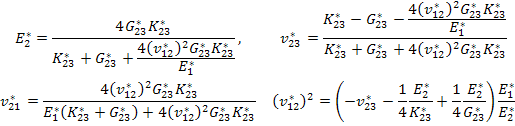 |
(7.167) |
Thus, if we know the effective engineering constants 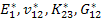 and and 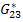 , then we can find the effective stiffness coefficients for transversely isotropic material. Further, the remaining engineering constants can also be determined. , then we can find the effective stiffness coefficients for transversely isotropic material. Further, the remaining engineering constants can also be determined.
The effective stiffness can be determined from the composite cylinder either using the concept of equivalence of strain energy or the basic definitions for each of the engineering property. For the equivalence of strain energy approach the strain energy of the composite cylinder must be equal to the strain energy of the single homogeneous cylinder. The strain energy in a given volume of the cylinder is given as
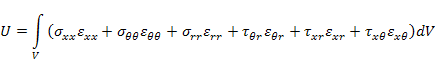 |
(7.168) |
In the case of a composite cylinder, the integral over volume extends over the volume of the core cylinder plus the volume of the annulus and in case of homogeneous cylinder it is over the one cylinder. It should be noted that both cylinder systems are subjected to same deformations. This approach can be complicated in the case of concentric cylinders as it involves both the geometry and elastic properties of two cylinders.
In the following sections we derive the effective engineering constants using the CCA model and basic definitions of engineering properties as follows. In this, the concentric cylinders are axially loaded. The composite axial modulus can be defined as axial force divided by axial strain produced by this axial force. Further, in this loading the assumption is that no other stresses are applied and the cylinders are free to deform.
|