|
Similarly, we define the following the Poisson’s ratios 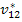 and and 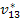 as as
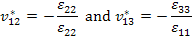 |
(7.153) |
Thus, using Equation (7.149), we get
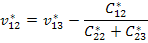 |
(7.154) |
The other engineering constants that can be directly related to the effective stiffness coefficients are
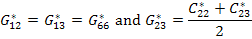 |
(7.155) |
Equations (7.152), (7.154) and (7.155) are four equations with five effective stiffness constants. We need one more equation in effective stiffness constants that relates an effective engineering constant. Then we can solve for 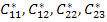 and and 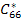 in terms of effective engineering constants. in terms of effective engineering constants.
We develop this equation as follows. Let us define the plane strain bulk modulus, 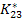 corresponding to the state of strain corresponding to the state of strain
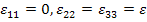 |
(7.156) |
For this state of strain, from the constitutive equation in Equation (7.148) the normal stresses are given as
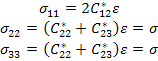 |
(7.157) |
Let us define 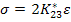 where where
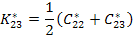 |
(7.158) |
is defined as effective plane strain bulk modulus.
Now, Equations (7.152), (7.154), (7.155) and (7.158) can be inverted to give
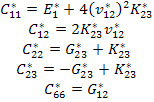 |
(7.159) |
In the above exercise, the measurable properties are 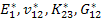 and and 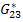 . However, one can measure the other engineering properties and express the effective stiffness coefficients. Let us consider that a uniaxial tension normal to the fibre direction is applied such that . However, one can measure the other engineering properties and express the effective stiffness coefficients. Let us consider that a uniaxial tension normal to the fibre direction is applied such that 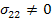 and and 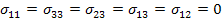 . Putting this in Equation (7.148) we can solve for the normal strains. The normal strains in terms of . Putting this in Equation (7.148) we can solve for the normal strains. The normal strains in terms of 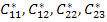 and and 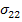 are given as are given as
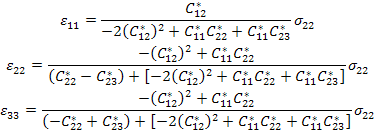 |
(7.160) |
From the second of the above equation, we can write
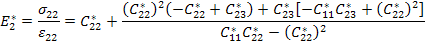 |
(7.161) |
|