Background of CCA Model
Here, we will relate five effective independent stiffness coefficients with the measurable effective engineering constants. In the following, for a transversely isotropic material we derive relations between the stiffness coefficients and engineering constants.
The unidirectional fibrous composite is transversely isotropic in nature in plane perpendicular to fibre direction (or in plane perpendicular to the plane in which fibres are placed together). The stress strain relations for the transversely isotropic material in 23 plane is written as
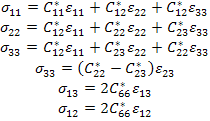 |
(7.148) |
Thus, there are five constants, 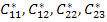 and and 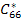 are independent constants. These constants define the effective properties of the composite. Note that in above relations tensorial shear strains are used. The relation between these independent constants and effective engineering constants can be given as follows: are independent constants. These constants define the effective properties of the composite. Note that in above relations tensorial shear strains are used. The relation between these independent constants and effective engineering constants can be given as follows:
Consider an uniaxial stress state such that 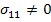 and and 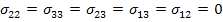 . .
. Putting this in Equation (7.148) we can solve for the normal strains. The normal strains in terms of 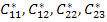 and and 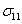 are given as are given as
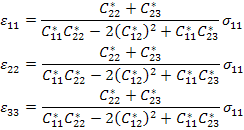 |
(7.149) |
From the first of the above equation, we can write
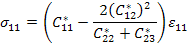 |
(7.150) |
We define the effective axial modulus 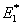 through following equation as through following equation as
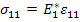 |
(7.151) |
Comparing this equation with Equation (7.150) we can write for 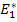 as as
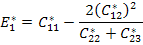 |
(7.152) |
|