The solution to this equation is
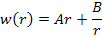 |
(7.174) |
Thus, the solution for fibre is
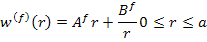 |
(7.175) |
and the solution for the matrix is
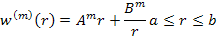 |
(7.176) |
The axial displacement in fibre and matrix can be determined by integrating the first of Equation (7.172) with respect to 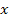 . In this equation the left hand side is independent of . In this equation the left hand side is independent of 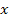 . .
Thus,
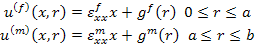 |
(7.177) |
It should be noted that 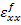 and and 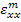 are constants and are constants and 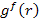 and and 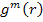 are the arbitrary constants of integration. The constants are the arbitrary constants of integration. The constants 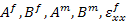 and and 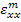 and functions and functions 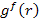 and and 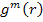 are unknown. These can be determined from specific boundary conditions. are unknown. These can be determined from specific boundary conditions.
The  displacement in fibre as given in Equation (7.175) should be bounded when displacement in fibre as given in Equation (7.175) should be bounded when 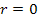 . This requires the condition that . This requires the condition that
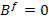 |
(7.178) |
Further, the displacements are continuous at the interface of fibre and matrix. This results in
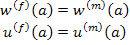 |
(7.179) |
Using Equation (7.178) and Equation (7.179), the continuity conditions become
 |
(7.180) |
On equating the terms in 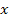 and and 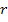 in the second of Equation (7.180), we get in the second of Equation (7.180), we get
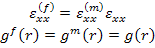 |
(7.181) |
This means that the strains in 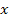 -direction in fibre and matrix are given by same function of -direction in fibre and matrix are given by same function of 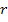 . Further, the unknown constant . Further, the unknown constant 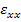 in fibre and matrix is same. This constant, in fact, is the axial strain. Therefore, it is denoted as in fibre and matrix is same. This constant, in fact, is the axial strain. Therefore, it is denoted as 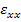 . .
|