|
Equation (7.130) can be simplified neglecting the terms of 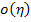 and higher order. Further, from Equation (7.131) we define the following strain tensors as and higher order. Further, from Equation (7.131) we define the following strain tensors as
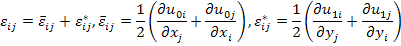 |
(7.132) |
where 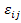 , as defined earlier, is the local or microstructural strain tensor, , as defined earlier, is the local or microstructural strain tensor, 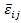 is the average or macroscopic strain tensor corresponding to the average displacements and is the average or macroscopic strain tensor corresponding to the average displacements and 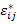 is fluctuating strain tensor corresponding to the oscillating displacements. As shown earlier, the fluctuating strain tensor is assumed to vary periodically. Now for the virtual displacement or weak form of the equilibrium equations let us assume that the virtual displacement is fluctuating strain tensor corresponding to the oscillating displacements. As shown earlier, the fluctuating strain tensor is assumed to vary periodically. Now for the virtual displacement or weak form of the equilibrium equations let us assume that the virtual displacement 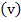 and hence the virtual strain and hence the virtual strain 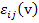 can also be expressed as asymptotic functions of can also be expressed as asymptotic functions of 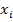 and and 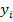 . Thus, the virtual strain is given as . Thus, the virtual strain is given as
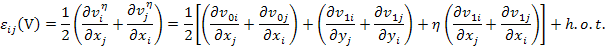 |
(7.133) |
Further, this strain can be written as average and microscopic strain due to virtual displacement as
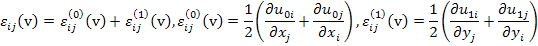 |
(7.134) |
The weak form of the equilibrium equations is given by
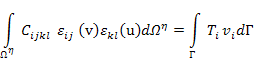 |
(7.135) |
Here, 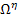 denotes the total, that is, macroscopic plus microscopic domain of the composite. The tractions denotes the total, that is, macroscopic plus microscopic domain of the composite. The tractions 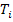 and the boundary displacements, if any, are applied only on the macroscopic boundaries of the composite. The first of Equation (7.132) and the first of Equation (7.134) are used in above equation. The resulting expanded form of the above equation is then given as and the boundary displacements, if any, are applied only on the macroscopic boundaries of the composite. The first of Equation (7.132) and the first of Equation (7.134) are used in above equation. The resulting expanded form of the above equation is then given as
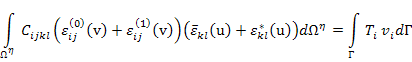 |
(7.136) |
|