Figure 7.9: (a) A bar representing alternate fibre and matrix (b) actual and average strain (c) actual and average displacement and (d) periodic nature of displacement difference over RVE length |
Consider Figure 7.9. Figure 7.9 (a) represents a bar with alternating materials. This bar represents alternate arrangement of fibre and matrix material in cross section. Let 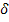 be the RVE length such that be the RVE length such that 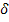 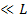 . Figure 7.9 (b) shows the variation of strain field. It should be noted that the strain in either of the element is constant and periodic in nature. However, the average strain in the bar is constant. Figure 7.9(c) shows the variation of actual displacement . Figure 7.9 (b) shows the variation of strain field. It should be noted that the strain in either of the element is constant and periodic in nature. However, the average strain in the bar is constant. Figure 7.9(c) shows the variation of actual displacement 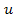 and average displacement field and average displacement field 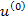 . From this figure it is clear that the actual displacement is oscillating around the average displacement. Figure 7.9 (d) shows the variation of . From this figure it is clear that the actual displacement is oscillating around the average displacement. Figure 7.9 (d) shows the variation of 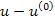 and one can easily notice that this variation is periodic over the RVE length. Thus, displacement and strain fields are varying over the two length scales, that is, at micro and macro scales. Further, the strain field and and one can easily notice that this variation is periodic over the RVE length. Thus, displacement and strain fields are varying over the two length scales, that is, at micro and macro scales. Further, the strain field and 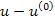 are periodic over the RVE. Thus, the problem of determining effective stiffness can be addressed by using the homogenization concept. The details of theory can be seen in [1-3]. are periodic over the RVE. Thus, the problem of determining effective stiffness can be addressed by using the homogenization concept. The details of theory can be seen in [1-3].
In the following we explain the theory of homogenization in brief.
Let 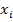 denote the global level or macro coordinates and denote the global level or macro coordinates and 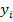 denote the micro level coordinates. These two level coordinates are related through denote the micro level coordinates. These two level coordinates are related through
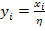 |
(7.128) |
Here 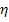 is the ratio of the RVE size to the size of the macroscopic region in which it exists. The field variables involved in this study are approximated by an asymptotic expansion as is the ratio of the RVE size to the size of the macroscopic region in which it exists. The field variables involved in this study are approximated by an asymptotic expansion as
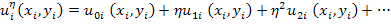 |
(7.129) |
where 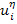 is the exact value of the field variable, is the exact value of the field variable, 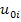 is the macroscopic or average value of the field variable. In elasticity theory, this is known as continuum level displacement field. The displacements is the macroscopic or average value of the field variable. In elasticity theory, this is known as continuum level displacement field. The displacements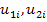 etc. are the perturbations in the field variable due to the microstructure. These are also called microstructural displacements. etc. are the perturbations in the field variable due to the microstructure. These are also called microstructural displacements.
Now, using the small deformations the strain tensor is written as
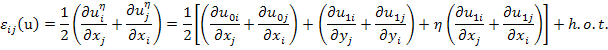 |
(7.130) |
In this derivation, the derivative of any function 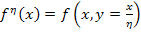 is given using chain rule as is given using chain rule as
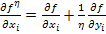 |
(7.131) |
has been used.
Note: The perturbation part of the solution is small, but clearly the corresponding strain is not. This strain is of the same order as the average strain.
Note: The quantities on the local level like stress vary  times more rapidly than the corresponding global level quantities. times more rapidly than the corresponding global level quantities. |