Homogenization
First, we will discuss the key points from statistical homogeneity and standard mechanics approach in the RVE analysis to determine the effective RVE properties. In micromechanical analysis most of the methods accurately predicts the effective composite properties provided that the ratio of the RVE size to the global structural dimension is very small tending to zero. In reference to Figure 7.9, we have 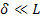 . We denote . We denote 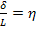 . .
In the micromechanics based methods the local level and global level analyses are decoupled. The local level analysis considers the microstructural details in its modeling. This analysis gives the effective elastic properties. Further, as we have seen in standard mechanics approach, the local level analysis can also be used to calculate the relationship of the effective or average RVE strain to the local strain within the RVE. However, the global level analysis is used to calculate the effective or the average stress and strain within the equivalent homogenous structure.
The process of calculating effective properties has been termed homogenization by Suquet [1]. Further, the local strains can be estimated from the relationship between average and local strains through local structure tensor obtained from local analysis. This process is called as localization.
In the RVE analysis the RVE is subjected to boundary condition. The solution of this boundary value problem gives the average properties along with the relation between the average and local strains. However, the accuracy of the results depends upon the fact that the applied boundary conditions should be able to reflect the in-situ (or the actual) boundary conditions to which an RVE is subjected. This is explained in the following paragraph.
Consider that the applied boundary conditions to the RVE which produce the same average strain in RVE are not same as the in-situ boundary conditions. Using the principle of minimum of strain energy the average stiffness predicted by the RVE analysis with assumed boundary conditions will be higher than that with in-situ boundary conditions. This is because the in-situ boundary conditions will minimize the strain energy. On the contrary, although the assumed boundary conditions are admissible they produce higher strain energy as the average stress produced is higher. Similarly, for the applied tractions by the principle of minimum of complementary energy the RVE analysis with applied homogeneous boundary produces higher complementary energy than that with in-situ boundary conditions. The applied boundary conditions would produce higher average stress in RVE than due to in-situ boundary conditions and also results in higher compliance. Thus, the RVE analyses with applied displacement boundary conditions give upper bound on effective stiffness whereas applied traction boundary conditions give the lower bound.
The homogenization theory is developed from studies of partial differential equations with rapidly varying coefficients. This theory is based on the two assumptions: the first one is that the fields vary on multiple scales due to existence of a microstructure and second one is that the microstructure is spatially periodic.
In the composite, it is well known to us that the microstructure is spatially periodic. Now in the following we explain that the displacement field is oscillating around the mean displacement and strain field is periodic over this microstructure. Further, the displacement and strain fields are varying over the two length scales.
|