|
Standard Mechanics Approach:
In this approach the standard mechanics based problems imposed on an RVE are solved. There can be two types of loads: displacements or tractions. The boundary conditions that are imposed on RVE are such that in case of displacement loading an average strain is produced in homogeneous material of same size as the RVE. While in case of traction loading, the boundary conditions are chosen such that an average stress is produced in homogeneous material of same size as the RVE.
The average strain as defined in Equation (7.75) is further written in terms of displacements using divergence theorem as
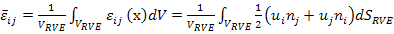 |
(7.89) |
where, 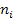 denotes the unit normal to the RVE boundary and other quantities are as defined earlier. Now, let us write the average stress in Equation (7.74) as denotes the unit normal to the RVE boundary and other quantities are as defined earlier. Now, let us write the average stress in Equation (7.74) as
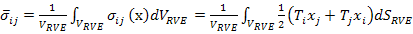 |
(7.90) |
where, 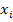 denotes the local boundary coordinates. For more details of the above derivation one can see work due to Hill [4]. denotes the local boundary coordinates. For more details of the above derivation one can see work due to Hill [4].
Now the important task is to choose the boundary conditions that will give us either averages strain or stress for displacement or traction loading. However, there is no unique relationship either between average strain and displacements or average stress and tractions. For example, a number of different combinations of displacements can produce the same average strain. Similarly, for the average stress in the material case there can be different combinations of tractions. Thus, in general, a uniform displacement or traction loading is chosen as boundary condition. These boundary conditions are shown in Figure 7.9. It should be noted that the applied boundary condition shown in this figure is displacement when average strain is desired and is traction if average stress is desired. Further, it should be noted that the boundary conditions shown in this figure are for a planar problem.
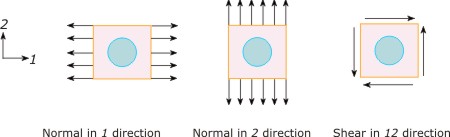 |
Figure 7.9: Uniform boundary conditions on an RVE |
|