Concept of Energy Equivalence:
The effective properties of composite are defined through Equation (7.76) using the average stress and strain in the RVE. One can propose the alternate definition of the effective properties using the concept of energy equivalence.
Let us write the Equation (7.76) by contracting it with average strain tensor 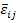 as as
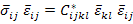 |
(7.78) |
It should be noted that the average stress and strain field used in Equation (7.78) are obtained by solving the problem with RVE applied by appropriate boundary conditions. The stresses and the strains in RVE are macroscopically homogeneous. Hence, the averages can also be obtained by boundary values instead of volume integrations. Thus, the left hand side of Equation (7.78) can be given in terms of surface tractions and displacements as
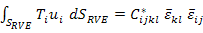 |
(7.79) |
where, 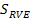 denotes the RVE boundary, denotes the RVE boundary, 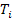 and and 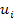 denote the traction and displacement vector on RVE boundary. Using the divergence theorem and equilibrium equations for the body without anybody forces, denote the traction and displacement vector on RVE boundary. Using the divergence theorem and equilibrium equations for the body without anybody forces, 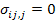 , we get , we get
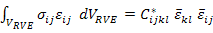 |
(7.80) |
Thus, the above relation gives the effective properties 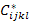 through the equivalence of the strain energy stored in the heterogeneous material to that stored in the equivalent homogeneous material. through the equivalence of the strain energy stored in the heterogeneous material to that stored in the equivalent homogeneous material.
In the following example, we explain concept of averaging. Consider the Figure 7.8(a). This figure represents the alternate repetition of two different materials with Young’s modulus 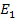 and and 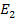 and and 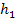 and and 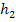 be their respective axial lengths. Further, let be their respective axial lengths. Further, let 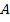 be the cross sectional area of the bar. This is equivalent to the alternate repetition of fibre and matrix in cross section. The bar made of such a material is subjected to axial force be the cross sectional area of the bar. This is equivalent to the alternate repetition of fibre and matrix in cross section. The bar made of such a material is subjected to axial force 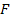 . From the equilibrium consideration between the interface of fibre and matrix, it is clear that the force is uniform throughout the bar as shown in Figure 7.8(b). Thus, the axial force in any section . From the equilibrium consideration between the interface of fibre and matrix, it is clear that the force is uniform throughout the bar as shown in Figure 7.8(b). Thus, the axial force in any section 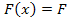 . The axial strain in each of the segment of the bar is given as . The axial strain in each of the segment of the bar is given as
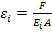 |
(7.81) |
From the above equation it is clear that the axial strains in fibre or matrix element are constants but there is a jump between interface of adjacent fibre and matrix. This is shown in Figure 7.8(c).
Now replace the material by an equivalent homogeneous material. Let 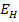 be the equivalent or homogeneous modulus of this material. Then, the force in equivalent material can be given as be the equivalent or homogeneous modulus of this material. Then, the force in equivalent material can be given as
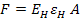 |
(7.82) |
Figure 7.8: (a) A beam representing alternate fibre and matrix (b) force distribution and (c) strain distribution along the length of the beam |
where, 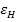 is the average or equivalent axial strain in the homogeneous material. Now, for a fibre and matrix element and its equivalent element the axial deformation is same. Thus, is the average or equivalent axial strain in the homogeneous material. Now, for a fibre and matrix element and its equivalent element the axial deformation is same. Thus,
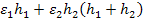 |
(7.83) |
Thus, from this equation we can write the average axial strain in the element as
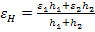 |
(7.84) |
Now, from Equation (7.82) and Equation (7.84) we can give the equivalent axial Young’s modulus as
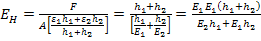 |
(7.85) |
In the above derivation Equation (7.81) has been used. Thus, Equation (7.85) gives the equivalent axial Young’s modulus based on equilibrium considerations.
Now we will use the equivalence of strain energy approach to derive the equivalent axial Young’s modulus. Let us consider that the fibre and matrix materials are linear elastic in behaviour. The strain energies of the non-homogeneous and homogeneous materials are equated as follows:
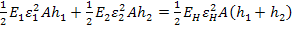 |
(7.86) |
Using Equation (7.81), we get
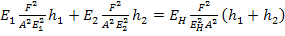 |
(7.87) |
which upon simplification gives us
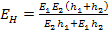 |
(7.88) |
Thus, Equation (7.88) gives the equivalent axial Young’s modulus based on energy equivalence approach.
Note: In the above example, the equilibrium approach and energy equivalence approach gave the same expression for effective axial Young’s modulus. However, for other examples and geometric details the effective properties obtained at the end may be different. |