|
The standard weak form of the equilibrium equation is solved to calculate the local RVE strain. In case of the applied displacements, the weak form of the RVE equilibrium equations is
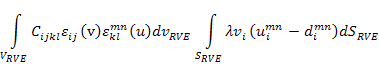 |
(7.91) |
where, 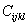 is the point-wise stiffness tensor in the RVE materials, is the point-wise stiffness tensor in the RVE materials, 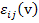 are the virtual strains, are the virtual strains, 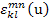 are the microstructural strains due to the applied displacements, are the microstructural strains due to the applied displacements, 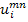 is the applied displacement, is the applied displacement, 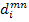 is the specified boundary displacement which produces the desired uniform average strain is the specified boundary displacement which produces the desired uniform average strain 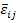 in a homogeneous material and in a homogeneous material and 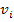 is the virtual displacement. Here, the boundary displacements are implemented using a penalty method with is the virtual displacement. Here, the boundary displacements are implemented using a penalty method with 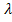 as the penalty parameter. as the penalty parameter.
In case of applied tractions the weak form the equilibrium equation to be solved for each applied mnth stress component is
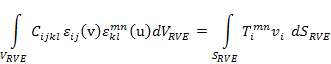 |
(7.92) |
where, 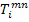 is the applied traction which produces the average stress is the applied traction which produces the average stress 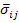 in a homogeneous material. Further, in a homogeneous material. Further, 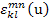 are the microstructural strains due to the applied mnth traction. The other terms in above equation are as defined earlier. are the microstructural strains due to the applied mnth traction. The other terms in above equation are as defined earlier.
Equation (7.91) and Equation (7.92) need to be solved only for three times. In these two equations we solve for local or microstructural strains. In this case we are considering symmetry of stress and strain tensors. In case of three dimensional problems we need to solve for six problems.
The relation between the average strain and local or microstructural strains is given as
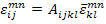 |
(7.93) |
where, 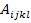 is called as local structure tensor or strain concentration factors. It should be noted that this tensor has minor symmetries like is called as local structure tensor or strain concentration factors. It should be noted that this tensor has minor symmetries like 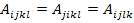 . .However, it does not have the major symmetry . .However, it does not have the major symmetry 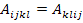 .. Thus, if the local structure tensor is known then local strain at any point can be given as .. Thus, if the local structure tensor is known then local strain at any point can be given as
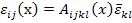 |
(7.94) |
Now the effective stiffness tensor 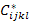 is as defined by Equation (7.76). This tensor can be calculated from is as defined by Equation (7.76). This tensor can be calculated from 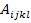 . Using the Hooke’s law at microscopic level, we can write . Using the Hooke’s law at microscopic level, we can write
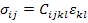 |
(7.95) |
Now, using the definition of average stress as in Equation (7.74), the above equation can be written as
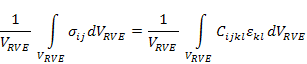 |
(7.96) |
Now using Equation (7.94) for 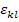 the above equation becomes the above equation becomes
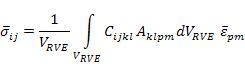 |
(7.97) |
Now, it should be noted that 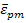 is the average strain. is the average strain.
Thus, we can define the effective stiffness tensor as
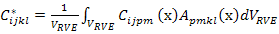 |
(7.98) |
The tensors 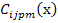 and and 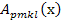 are the local tensors and can be obtained in individual constituents of the RVE. Once, the effective stiffness tensor is obtained the inverse of this gives the effective compliance tensor. Now the relation between the individual elements of this tensor and engineering constants can be used to determine the effective engineering constants. are the local tensors and can be obtained in individual constituents of the RVE. Once, the effective stiffness tensor is obtained the inverse of this gives the effective compliance tensor. Now the relation between the individual elements of this tensor and engineering constants can be used to determine the effective engineering constants. |