Coefficients of Hygral Expansion 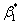 and and 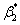 : :
When the composite is subjected to hygroscopic environment, it absorbs the moisture and deforms. It should be noted that the deformation of the fibre and matrix depends upon the amount of moisture absorbed. Further, the amount of moisture absorbed by fibre and matrix in same environment are, in general, not same. It will be shown that, unlike the coefficients of thermal expansion, the moisture content will enter into the expressions of coefficients of hygral expansion of composite.
The derivation also follows similar procedure as used in the derivation of coefficients of thermal expansion. The deformation constraints, similar to the derivation of coefficients of thermal expansion, are also imposed in this derivation.
The force in axial direction in composite should be zero. This condition leads to the equation
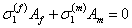 |
(7.64) |
The axial stresses in fibre and matrix due to moisture absorption alone are given as
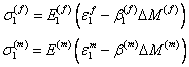 |
(7.65) |
where, 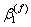 and and  are the coefficients of hygral expansion of fibre and matrix, respectively. are the coefficients of hygral expansion of fibre and matrix, respectively. 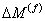 and and 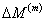 are the per weight % moisture absorption for fibre and matrix, respectively. Putting this in Equation (7.64) and knowing that the axial strain in fibre and matrix are equal, that is, are the per weight % moisture absorption for fibre and matrix, respectively. Putting this in Equation (7.64) and knowing that the axial strain in fibre and matrix are equal, that is, 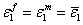
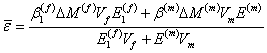 |
(7.66) |
The effective coefficient of hygral expansion in axial direction is defined as
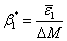 |
(7.67) |
where, 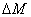 is the per weight % moisture absorption for composite. Thus, the above equation becomes is the per weight % moisture absorption for composite. Thus, the above equation becomes
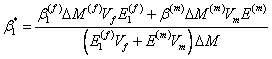 |
(7.68) |
The above equation can be further simplified by expressing the percentage weight moisture absorbed by composite to the moisture absorbed by fibre and matrix. Thus,
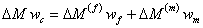 |
(7.69) |
where, 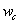 , , 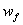 and and 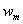 are the masses (as defined earlier) of composite, fibre and matrix, respectively. The above equation can be written as are the masses (as defined earlier) of composite, fibre and matrix, respectively. The above equation can be written as
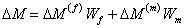 |
(7.70) |
Thus, Equation (7.68) becomes
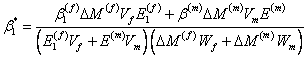 |
(7.71) |
The mass fractions are written in terms of volume fractions with the use of densities of composite, fibre and matrix. Then the above equation becomes
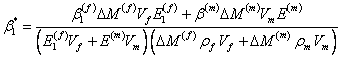 |
(7.72) |
The coefficient of thermal expansion in transverse direction, 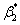 is given as is given as
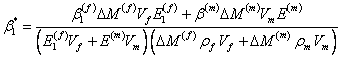 |
(7.73) |
|