Now it should be noted that due to temperature change the force in direction 1 should be zero. Further, the stresses in transverse direction in fibre and matrix should be identically zero. The first condition leads to
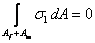 |
(7.57) |
Further, assuming that the stresses in fibre and matrix are uniform, the above equation becomes
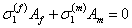 |
(7.58) |
The second condition that the stresses in transverse direction are zero leads to
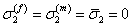 |
(7.59) |
Putting the first of Equation (7.55) and Equation (7.56) in Equation (7.58), we get
 |
(7.60) |
Using the second of Equation (7.55) and Equation (7.56) in Equation (7.59), we get
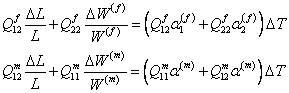 |
(7.61) |
Thus, Equation (7.60) and Equation (7.61) are three simultaneous equations in 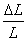 , , 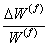 and and 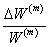 . We solve these three equations and define the coefficients of thermal expansions for composites as . We solve these three equations and define the coefficients of thermal expansions for composites as
 |
(7.62) |
and
 |
(7.63) |
The above expressions are the rule of mixture for coefficients of thermal expansions for composite in terms of individual coefficients of thermal expansion, volume fractions and other properties. In the above equation 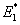 is the effective axial modulus, as given earlier. Comparing Equation (7.54) and Equation (7.63), it is clear that the last term in Equation (7.63) is due to the imposition of deformation constraint under thermal loading. is the effective axial modulus, as given earlier. Comparing Equation (7.54) and Equation (7.63), it is clear that the last term in Equation (7.63) is due to the imposition of deformation constraint under thermal loading.
|