|
Coefficients of Thermal Expansion 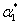 and and 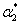 : :
The coefficients of thermal expansion are very important as the composite is fabricated as elevated temperature and cooled down to room temperature. In this process, due to difference in the coefficients of thermal expansion of fibre and matrix materials, the thermal residual stresses are developed. The determination of the coefficients of thermal expansion of the composite is dealt in this section.
First, we will derive an expression for the coefficients of thermal expansion in transverse direction, 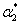 . We will use the deformation same as shown in Figure 7.5. The only difference is that the effective stress in transverse direction must be zero. This is because that the thermal expansion should occur without any applied stress. Thus, for the deformations as shown in Figure 7.5, we take . We will use the deformation same as shown in Figure 7.5. The only difference is that the effective stress in transverse direction must be zero. This is because that the thermal expansion should occur without any applied stress. Thus, for the deformations as shown in Figure 7.5, we take 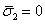 . Now the deformation in fibre and matrix in transverse direction can be given as . Now the deformation in fibre and matrix in transverse direction can be given as
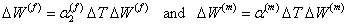 |
(7.51) |
where, 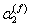 is the coefficient of thermal expansion of fibre in transverse direction and is the coefficient of thermal expansion of fibre in transverse direction and 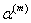 is the coefficient of thermal expansion of matrix. It should be noted that the matrix is assumed to be isotropic in nature. is the coefficient of thermal expansion of matrix. It should be noted that the matrix is assumed to be isotropic in nature. 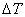 is increase in temperature. Let us define the coefficient of expansion for composite in transverse direction, is increase in temperature. Let us define the coefficient of expansion for composite in transverse direction, 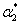 as as
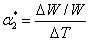 |
(7.52) |
Using Equation (7.51) in above equation, we get
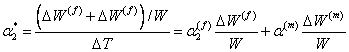 |
(7.53) |
Thus, using the volume fraction definitions, we get
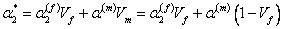 |
(7.54) |
This is the rule of mixtures for the transverse coefficient of thermal expansion. It should be noted that in this derivation the interaction between fibre and matrix under the temperature effect is not constant. Thus, this derivation neglects the thermally induced stresses in fibre and matrix. However, this is not true as thermal stresses will be induced in fibre and matrix. We take into account this fact and derive alternate expression for this coefficient of thermal expansion as follows.
The stresses in fibre can be given for the temperature change of 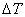 as as
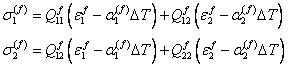 |
(7.55) |
and in matrix can be given as
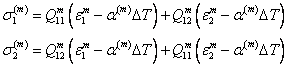 |
(7.56) |
|