|
Effective Axial Shear Modulus 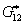 : :
To derive the effective axial shear modulus of the composite the RVE is loaded in shear as shown in Figure 7.6(a). The fibre and matrix are assumed to deform independently. Figure 7.6(b) shows the overall deformation of the RVE. The overall axial deformation is denoted by 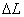 . It is important to note that for equilibrium considerations the shear stresses acting on fibre and matrix are assumed to be identical. . It is important to note that for equilibrium considerations the shear stresses acting on fibre and matrix are assumed to be identical.
Under the pure shear loading, that is, 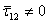 and other stress components are zero, the effective axial shear modulus is defined as and other stress components are zero, the effective axial shear modulus is defined as
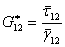 |
(7.45) |
Figure 7.6: (a) Undeformed unit cell under uniform 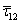 stress (b) overall deformation of unit cell (c) and (d) deformed individual constituents of the unit cell stress (b) overall deformation of unit cell (c) and (d) deformed individual constituents of the unit cell |
where, 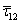 and and 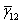 are the effective applied shear stress and the resulting effective shear strain in the composite, respectively. The effective shear strain in composite is obtained from the deformations of the fibre and matrix in RVE. The fibre and matrix undergo deformations are the effective applied shear stress and the resulting effective shear strain in the composite, respectively. The effective shear strain in composite is obtained from the deformations of the fibre and matrix in RVE. The fibre and matrix undergo deformations 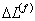 and and 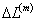 , respectively. These deformations are shown in Figure 7.6(c) and (d), respectively. , respectively. These deformations are shown in Figure 7.6(c) and (d), respectively.
The shear strains in the fiber and matrix are given as
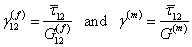 |
(7.46) |
where, 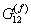 is the inplane shear modulus of the fibre and is the inplane shear modulus of the fibre and 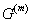 is the shear modulus of the matrix material. From Figure 7.6(c) and (d), we can write the individual deformations in fibre and matrix as is the shear modulus of the matrix material. From Figure 7.6(c) and (d), we can write the individual deformations in fibre and matrix as
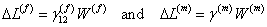 |
(7.47) |
Using Equation (7.46) in above equation, the total axial deformation is given as
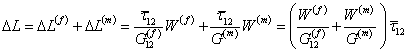 |
(7.48) |
Now, we can give the overall shear strain of the RVE as
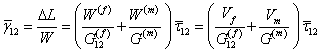 |
(7.49) |
Finally, the effective axial shear modulus of the composite can be given from above equation as
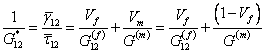 |
(7.50) |
This is the rule of mixtures equation for the effective axial shear modulus. This equation is analogous to Equation (7.33) for the effective transverse modulus of the composite.
|