Generally, the stresses are uniform in the fibre and matrix. Thus above equation reduces to
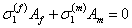 |
(7.37) |
Further, for equilibrium in transverse direction, we have
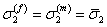 |
(7.38) |
The axial and transverse strains in fibre and matrix are
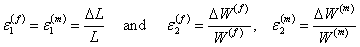 |
(7.39) |
Using Equations (7.34) and (7.39) in (7.37), we get
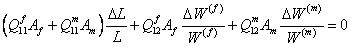 |
(7.40) |
Further, using Equation (7.34) in Equation (7.38), we get
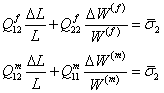 |
(7.41) |
We solve Equations (7.40) and (7.41) for 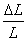 , , 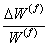 and and 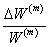 . The transverse composite strain then is obtained as . The transverse composite strain then is obtained as
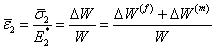 |
(7.42) |
Finally, putting the values of 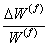 and and 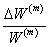 in the above equation, we get an expression for in the above equation, we get an expression for 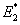 as as
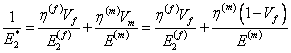 |
(7.43) |
where,
 |
(7.44) |
Equation (7.43) is an alternate equation for effective transverse modulus 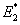 . This is also a rule of mixtures equations. It should be noted that the factors . This is also a rule of mixtures equations. It should be noted that the factors 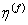 and and 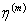 are the nondimensional factors. are the nondimensional factors. |