Effective Transverse Modulus 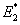 : :
In the earlier lecture we have seen the first approach, where the deformation of individual constituent is independent of each other and the deformation in direction 1 is not considered. In this lecture we are going to derive an expression for effective transverse modulus using second approach as follows.
Second Approach:
In this approach, we consider the resulting deformation in direction 1. It should be noted that when the stress is applied in direction 2, the deformations of fibre and matrix in direction 1 are identical. The deformation in direction 1 is calculated from two dimensional state of stress in fibre and matrix. The deformations are shown in Figure 7.5.
The axial and transverse stresses in fibre and matrix can be given using planar constitutive relations as
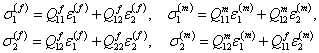 |
(7.34) |
where,
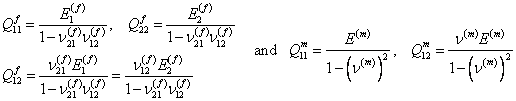 |
(7.35) |
To compute the effective transverse modulus 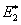 we need to find the total deformation we need to find the total deformation 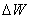 as a function of the applied transverse stress as a function of the applied transverse stress 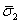 . It should be noted that the net force in the direction 1 is zero. Thus, . It should be noted that the net force in the direction 1 is zero. Thus,
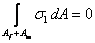 |
(7.36) |
Figure 7.5: (a) Undeformed unit cell under uniform 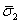 stress (b) and (c) deformed individual constituents of the unit cell stress (b) and (c) deformed individual constituents of the unit cell |
|