| |
Likewise, if we apply stress states as 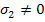 and and 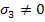 with other stresses being zero, it will give us the following constants: with other stresses being zero, it will give us the following constants:
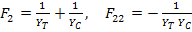 |
(6.47) |
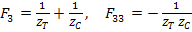 |
(6.48) |
Similarly, if we apply 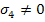 , , 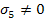 , , 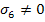 and with other stress components as zero, as three separate states of stress, then we get following constants: and with other stress components as zero, as three separate states of stress, then we get following constants:
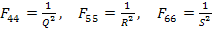 |
(6.49) |
So far we have developed expressions for 3 strength terms for 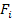 and diagonal terms of and diagonal terms of 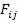 . Now the expressions for off-diagonal terms of . Now the expressions for off-diagonal terms of 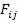 require combined state of stress to be applied. The pure axial or shear state of stress will not be sufficient. In other criteria the interaction terms like require combined state of stress to be applied. The pure axial or shear state of stress will not be sufficient. In other criteria the interaction terms like 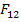 are assumed to be dependent or terms like are assumed to be dependent or terms like 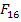 are zero. are zero.
There are an infinite combinations of the stresses from which these terms can be obtained. However, one should choose those combinations which can yield the desired result in a reliable and easy manner. In the following, we will see typical combinations of stresses to find 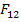 . .
Consider the equivi-biaxial stress state 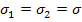 and other stress components are zero. Putting this in Equation (6.43), we get and other stress components are zero. Putting this in Equation (6.43), we get
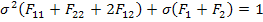 |
(6.50) |
Solving for 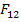 , we get , we get
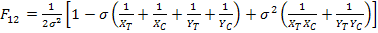 |
(6.51) |
Similarly, if we apply equivi-biaxial stress states in 1-3 and 2-3 planes, then we get the following constants:
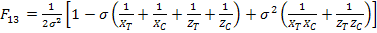 |
(6.52) |
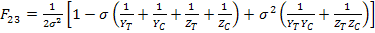 |
(6.53) |
We can find the constants 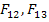 and and 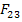 by imposing the equivi-biaxial state of stress. However, practically it is very difficult to impose such a state of stress. Hence, many researchers have proposed tests on by imposing the equivi-biaxial state of stress. However, practically it is very difficult to impose such a state of stress. Hence, many researchers have proposed tests on 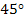 angle specimens to determine these strength parameters. angle specimens to determine these strength parameters.
|