|
Consider the stress state
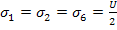 |
(6.54) |
and other stresses are zero. Here, 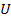 is the axial tensile strength of is the axial tensile strength of  specimen. The stress state in Equation (6.54) is obtained by applying specimen. The stress state in Equation (6.54) is obtained by applying  in axial direction for in axial direction for 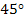 specimen. One should be able to get the state of stress in Equation (6.54) from our earlier stress transformation equations. Putting Equation (6.54) in Equation (6.43), we get specimen. One should be able to get the state of stress in Equation (6.54) from our earlier stress transformation equations. Putting Equation (6.54) in Equation (6.43), we get
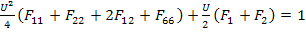 |
(6.55) |
which upon solving for 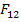 gives gives
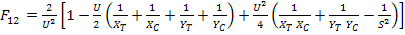 |
(6.56) |
A similar expression can be derived with compressive strength of 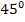 specimen. One can further find this constant using the in-plane shear strength of specimen. One can further find this constant using the in-plane shear strength of 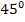 specimen, specimen, 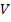 which produces the stress state as which produces the stress state as
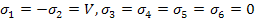 |
(6.57) |
This reduces Equation (6.43) to
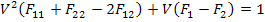 |
(6.58) |
The solution 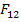 from this equation is from this equation is
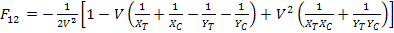 |
(6.59) |
Note: In case of anisotropic materials the constant 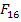 is no longer zero. This can be obtained by a tension-torque test such that it results in following stress state is no longer zero. This can be obtained by a tension-torque test such that it results in following stress state
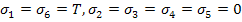 |
(6.60) |
Using this in Equation (6.43), we get
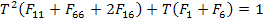 |
(6.61) |
which gives
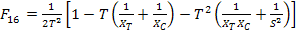 |
(6.62) |
The Tsai-Wu criterion for planar state of stress can be given as
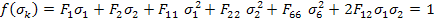 |
(6.63) |
The strength parameters are as given above. If the strength term 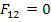 then, the criterion becomes then, the criterion becomes
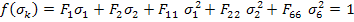 |
(6.64) |
|