|
Now we will seek simplifications to Equation (6.36) as follows. The strength tensors can be written in the form
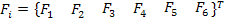 |
(6.41) |
and
 |
(6.42) |
where, both strength tensors are assumed to be symmetric with 6 and 21 independent constants for 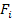 and and 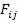 , respectively. , respectively.
The number of independent strength parameters can be further reduced if we have some form of material symmetry. We consider a special case of specially orthotropic material. Thus, for specially orthotropic material the terms 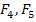 and and 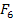 will vanish. Further, the off-diagonal terms which give normal shear coupling like will vanish. Further, the off-diagonal terms which give normal shear coupling like 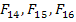 , etc. will also become zero if we assume that the sign of shear stress does not change the failure stress. Further, with same reasoning we assume that the shear strengths are also uncoupled leading to , etc. will also become zero if we assume that the sign of shear stress does not change the failure stress. Further, with same reasoning we assume that the shear strengths are also uncoupled leading to 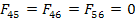 . Thus, with this material symmetry, we have . Thus, with this material symmetry, we have
The number of independent strength parameters are now 3 and 9 for 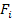 and and 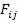 , respectively. Thus, for orthotropic material the criterion becomes , respectively. Thus, for orthotropic material the criterion becomes
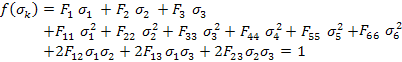 |
(6.43) |
Now we will determine the strength parameters by thought experiments. First, we apply 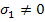 and other stress components being zero. For this state of stress, the failure in tension requires and other stress components being zero. For this state of stress, the failure in tension requires 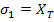 . Thus, Equation (6.43) becomes . Thus, Equation (6.43) becomes
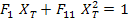 |
(6.44) |
Similarly, for this state of stress, the failure in compression requires 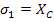 . This results in Equation (6.43) to become . This results in Equation (6.43) to become
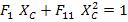 |
(6.45) |
Equation (6.44) and Equation (6.45) are two simultaneous equations with 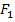 and and 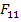 as two unknowns. as two unknowns. Solution of these two equations gives
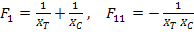 |
(6.46) |
|