-
The resulting criterion is a scalar function and thus an invariant. Further, the interactions between various components are independent unlike in Tsai-Hill theory where interactions are fixed and in case of maximum stress or maximum strain theory these interactions are not possible.
-
The strength components are expressed as tensors; one can use the transformation rules as discussed earlier for their transformations. Further, the invariants of these strength tenors are also well defined.
-
The property of symmetry of strength tenors and number of independent and non-zero components can be derived in similar way that we carried out for anisotropic materials earlier.
-
One can either transform the strength parameters from 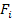 to
to 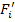 and
and 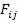 to
to 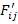 or transform
or transform 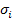 to
to 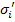 . Most of the existing criteria are limited to specially orthotropic materials. Such criteria can be applied only by transforming the external stresses to material axes. However, the transformations of strength criteria cannot be done as this transformation is not known.
. Most of the existing criteria are limited to specially orthotropic materials. Such criteria can be applied only by transforming the external stresses to material axes. However, the transformations of strength criteria cannot be done as this transformation is not known.
-
Since Equation (6.36) is an invariant, hence, an invariant for any other coordinate system. This also holds for curvilinear coordinate system as well.
-
The theory has also introduced constraints over the magnitude of the strength interaction terms in the following manner
:
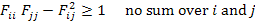 |
(6.37) |
The terms 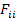 represent diagonal terms and are positive terms, whereas the off-diagonal terms can be positive or negative depending upon their interaction with other terms. However, their magnitudes are constrained by Equation (6.37). Further, the inequality in Equation (6.37) is very important as it assures the failure envelope in Equation (6.35) intersects all stress axes. The surface formed by Equation (6.35) is an ellipsoid and Equation (6.37) ensures that it is a closed surface unlike a hyperboloid. It should be noted that the positive definiteness is also imposed for
represent diagonal terms and are positive terms, whereas the off-diagonal terms can be positive or negative depending upon their interaction with other terms. However, their magnitudes are constrained by Equation (6.37). Further, the inequality in Equation (6.37) is very important as it assures the failure envelope in Equation (6.35) intersects all stress axes. The surface formed by Equation (6.35) is an ellipsoid and Equation (6.37) ensures that it is a closed surface unlike a hyperboloid. It should be noted that the positive definiteness is also imposed for 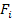 terms.
terms.
-
Gol’denbalt and Kopnov [3] proposed a tensorial criterion in a general form of
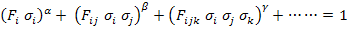 |
(6.38) |
This form of the equation is more complicated than in Equation (6.35). Further, the size of the strength terms is enormously very high to handle and the additional terms do not yield more generality than the linear and quadratic terms.
Note: Statement 4 above equivalently says that the Tsai-Wu strength criterion can be given in transformed coordinate system. The transformed criterion may be given as
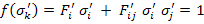 |
(6.39) |
And the strength terms can be transformed using the following relations
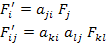 |
(6.40) |
However, the transformation of any other strength criteria may not hold true.