4. Hoffman Theory
The Hoffman criterion [1] is extension of Tsai-Hill theory. In Tsai-Hill theory the strength parameters are obtained without considering the difference in values in tension and compression. However, one should realistically consider the differing tension and compression strengths that characterize brittle behaviour. This can be done by adding odd functions of 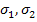 and and 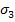 in the expression of Tsai-Hill criterion. Thus, Equation (6.13) becomes in the expression of Tsai-Hill criterion. Thus, Equation (6.13) becomes
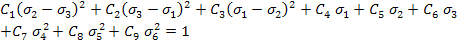 |
(6.24) |
where, 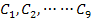 are the material parameters. These are uniquely determined from nine basic strength data, namely, three uniaxial tensile strengths, are the material parameters. These are uniquely determined from nine basic strength data, namely, three uniaxial tensile strengths, 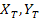 and and 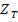 ; three uniaxial compressive strengths, ; three uniaxial compressive strengths, 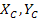 and and 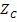 and three shear strength parameters, Q, R and S. To determine these material strength parameters, we need to do thought experiments as follows: and three shear strength parameters, Q, R and S. To determine these material strength parameters, we need to do thought experiments as follows:
First, consider the state of stress such that 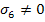 and all other stress components will be zero. For shear failure in this mode, we need and all other stress components will be zero. For shear failure in this mode, we need 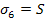 . Putting this in Equation (6.24), we get . Putting this in Equation (6.24), we get
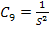 |
(6.25) |
Similarly, we get the constants
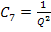 |
(6.26) |
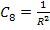 |
(6.27) |
Now, to find remaining constants we apply following state of stress. Let 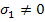 and all other stress components be zero. For tensile failure, we need and all other stress components be zero. For tensile failure, we need 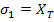 for this stress state. Putting this in Equation (6.24) we get for this stress state. Putting this in Equation (6.24) we get
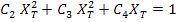 |
(6.28) |
Similarly for this stress state, the compression failure requires 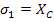 . This results the Equation (6.24) to give . This results the Equation (6.24) to give
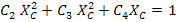 |
(6.29) |
Now, we have two stress states: First one as 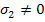 and all other stress components are zero and the second one as and all other stress components are zero and the second one as 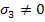 and all other stress components are zero. Again, as in previous case for failure in tension and compression, Equation (6.24) results into following conditions: and all other stress components are zero. Again, as in previous case for failure in tension and compression, Equation (6.24) results into following conditions:
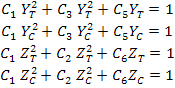 |
(6.30) |
Thus, Equations (6.28), (6.29) and (6.30) give a set of six simultaneous equations in 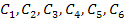 . Solving these, we get . Solving these, we get
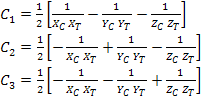 |
(6.31) |
and
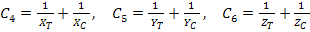 |
(6.32) |
Thus, the Hoffman criterion as given in Equation (6.24) becomes
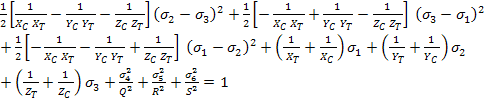 |
(6.33) |
Now consider transverse isotropy of the material in 2-3 plane. Thus, 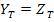 and and 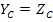 . For shear strength, we have . For shear strength, we have 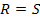 . Then for plane stress condition . Then for plane stress condition 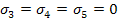 , the criterion in Equation. (6.33) becomes , the criterion in Equation. (6.33) becomes
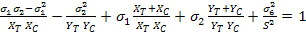 |
(6.34) |
Equation (6.34) represents Hoffman criterion for planar state of stress in transversely isotropic materials. It should be noted that in this criterion there is no need to check the sign of the stress components to decide whether a tensile or compressive strength is to be used.
|