3. Tsai-Hill Theory:
This theory is an extension of distortional energy yield criterion of von-Mises [3] for isotropic materials as applied to anisotropic materials. It is known that total strain energy in a body is composed of two parts: One is distortion energy which cause change in shape and second one is dilation energy which causes the change in size or volume. In the von-Mises criterion it is assumed that the material fails when the maximum distortion energy of the body exceeds the distortion energy corresponding to yielding of the same material in tension.
Hill [4] extended the von-Mises distortion energy criterion of isotropic materials to anisotropic materials. Later Tsai [5, 6] extended this criterion for anisotropic materials to a unidirectional lamina. Hence, the theory is called Tsai-Hill theory.
According to this theory the failure takes place when the stress state is such that
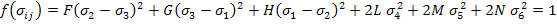 |
(6.13) |
which upon simplifications can be written as
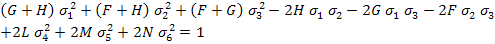 |
(6.14) |
where, F, G, H, L, M and N are the material strength parameters. Thus, any state of stress which lies inside this envelope is safe and the one which lies on or outside the envelope is unsafe.
The strength parameters correspond to failure stresses in one dimensional loading. These can be obtained by a set of thought experiments. For example, consider that for the pure shear loading in 2-3 plane, that is with 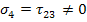 , with corresponding shear strength Q and all other stress components are zero, the Equation (6.14) becomes , with corresponding shear strength Q and all other stress components are zero, the Equation (6.14) becomes
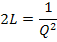 |
(6.15) |
Similarly, for the other two shear stress components, we can get
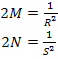 |
(6.16) |
Now the strength parameters F, G and H are obtained by three states of stress. The state of stress 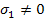 with corresponding strength X and all other stress components being zero, in Equation (6.14) leads to with corresponding strength X and all other stress components being zero, in Equation (6.14) leads to
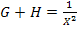 |
(6.17) |
Now the conditions 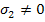 and and 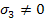 (and other stress components being zero) in Equation (6.14) result in (and other stress components being zero) in Equation (6.14) result in
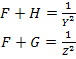 |
(6.18) |
solving the simultaneous equations in Equation (6.17) and Equation (6.18), we get the required strength parameters as
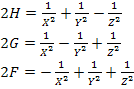 |
(6.19) |
Thus, Equation (6.14) becomes
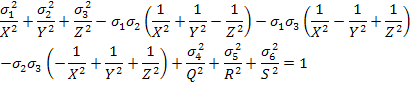 |
(6.20) |
This is Tsai-Hill theory for 3D state of stress. Note that this is quadratic in stress terms with no linear terms.
|