Now consider a transversely isotropic material with inplane stresses as the significant stresses. For this planar state of stress, we have 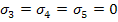 and remaining stress components are non zero. In this case the failure envelope becomes a three dimensional space. Thus, the failure condition in Equation (6.14) becomes and remaining stress components are non zero. In this case the failure envelope becomes a three dimensional space. Thus, the failure condition in Equation (6.14) becomes
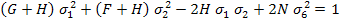 |
(6.21) |
Now, using the strength parameters from Equation (6.17), Equation (6.18) and Equation (6.19), we get
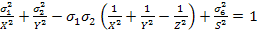 |
(6.22) |
For transverse isotropy, we also have 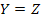 . Thus, the above equation is rearranged as . Thus, the above equation is rearranged as
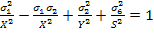 |
(6.23) |
The above equation gives the Tsai-Hill criterion for failure for planar state of stress. From Tsai-Hill theory it is clear that it does not differentiate between tension and compression strengths for normal stresses. Infact, Tsai-Hill theory assumes same strengths in tension and compression. However, this situation does not occur in case of shear stresses. Thus, for normal stresses the theory represents a severe limitation that the sign of the normal stresses should be known a priori and the appropriate strength value should be used for normal stresses in the failure theory.
It should be noted that unlike maximum stress theory or maximum strain theory Tsai-Hill theory considers the interaction between three lamina strength parameters or interaction between stress components.
Further, it should be noted that Tsai-Hill theory is a unified theory and does not give the mode of failure like the maximum stress and maximum strain theory. However, one can make a guess of failure mode by calculating the quantities 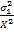 , , 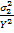 and and 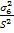 . The maximum of these three values can be said to give the mode of failure. . The maximum of these three values can be said to give the mode of failure.
Note: The right hand side of Equation (6.20) or (6.23) is called as “failure index”.
|