|
2. Maximum Strain Theory:
Maximum strain theory is equivalent to maximum stress theory. This theory is based on maximum normal strain theory of St. Venant and the strain equivalent of maximum shear stress theory of Tresca for isotropic materials.
According to this theory, a lamina fails if either of the normal strain exceeds the maximum allowable strain in tension or compression or any of the shear strain exceeds the maximum allowable shear strain. The inequalities resulting are:
For normal strains,
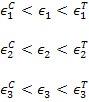 |
(6.8) |
For shear stresses,
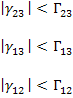 |
OR |
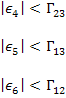 |
|
(6.9) |
where, 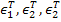 and and 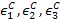 are the ultimate normal strains in tension and compression, respectively. Further, are the ultimate normal strains in tension and compression, respectively. Further, 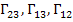 are ultimate shear strains in 23, 13, 12 planes, respectively. are ultimate shear strains in 23, 13, 12 planes, respectively.
Thus, according to this theory initiation of failure will correspond to one or more inequalities in Equations (6.8) and (6.9) become equality.
The maximum strain theory for planar stress can be expressed as
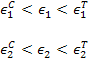 |
(6.10) |
and for shear strain as
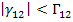 |
(6.11) |
The strains can be obtained from constitutive equation for strains in terms stresses as
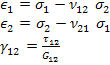 |
(6.12) |
These equations can be put in Equation (6.10) and Equation. (6.11). Further, for axial stress applied 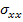 we can write the stresses in principal directions as in Equation (6.6). we can write the stresses in principal directions as in Equation (6.6).
Note: The maximum stress and maximum strain theories are similar. In both theories there is no interaction between various components of stress or strain. However, the two theories yield different results.
|