Cross-Ply Laminates:
A laminate is called cross-ply laminate if all the plies used to fabricate the laminate are only 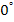 and and 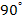
For example 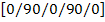 is shown in Figure 5.6 (b). is shown in Figure 5.6 (b).
For a cross ply laminate the terms 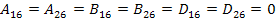 . This is because these terms involve the terms . This is because these terms involve the terms 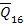 and and 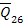 which have the products of mn terms. This product is zero for any cross-ply. Thus, the terms which have the products of mn terms. This product is zero for any cross-ply. Thus, the terms 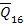 and and 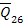 are identically zero for each ply. are identically zero for each ply.
Note: For a cross-ply following relations hold true. The readers should verify these relations from earlier lectures on planar constitutive relations.
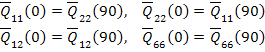 |
(5.51) |
Angle-Ply Laminates:
A laminate is called angle-ply laminate if it has plies of the same thickness and material and are oriented at 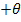 and and 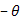 . For example . For example 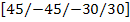 is shown in Figure 5.6(c). is shown in Figure 5.6(c).
For angle-ply laminates the terms 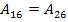 are zero. This can be justified by that fact that are zero. This can be justified by that fact that 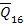 and and 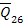 have the term mn. Due to this term have the term mn. Due to this term 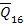 and and 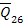 have opposite signs for layers with have opposite signs for layers with 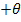 and and 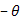 fibre orientation. Since the thicknesses and materials of these layers are same, by the definition the terms fibre orientation. Since the thicknesses and materials of these layers are same, by the definition the terms 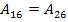 are zero for the laminate. are zero for the laminate.
Note: For angle-ply laminates the following relations are very useful in computing 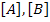 and and 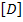 . .
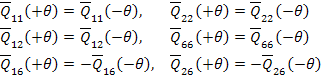 |
(5.52) |
Anti-symmetric Laminates:
A laminate is called anti-symmetric when the material and thickness of the plies are same above and below the mid-plane but the orientation of the plies at same distance above and below the mid-plane have opposite signs. For example, 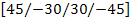 is shown in Figure 5.6(d). is shown in Figure 5.6(d).
For anti-symmetric laminates the terms 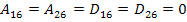 . The proof is left to the readers as an exercise. . The proof is left to the readers as an exercise.
Balanced Laminates:
A laminate is called balanced laminate when it has pairs of plies with same thickness and material and the angles of plies are 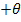 and and 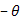 . However, the balanced laminate can also have layers oriented at . However, the balanced laminate can also have layers oriented at 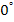 and and 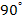 . For this laminate also . For this laminate also 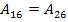 are zero. It should be noted that angle-ply laminates are balanced laminates. For example, are zero. It should be noted that angle-ply laminates are balanced laminates. For example, 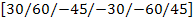 is shown in Figure 5.6(e). is shown in Figure 5.6(e).
|